發展歷史,表達方式,代數表示,幾何表示,坐標表示,行列式的幾何意義,相關定義,有向線段,向量的模,單位向量,負向量,零向量,相等向量,自由向量,滑動向量,固定向量,位置向量,方向向量,相反向量,平行向量,共面向量,法向量,向量的和的模,運算,加法,減法,數乘,數量積,向量積,三向量混合積,雙重向量積,關係式,兩個向量構成的平行四邊形的面積公式,向量定理,共線定理,垂直定理,分解定理,定比分點公式,三點共線定理,重心判斷式,垂心判斷式,內心判斷式,外心判斷式,向量空間,定義,同構,映射,延伸,子空間及基,向量的中線公式,
發展歷史 向量,最初被套用於物理學。很多
物理量 如力、速度、位移以及電場強度、
磁感應強度 等都是向量。大約公元前350年前,
古希臘 著名學者
亞里士多德 就知道了力可以表示成向量,兩個力的組合作用可用著名的
平行四邊形法則 來得到。“向量”一詞來自力學、解析幾何中的有向
線段 。最先使用有向線段表示向量的是英國大科學家
牛頓 。
向量 從數學發展史來看,歷史上很長一段時間,
空間 的向量結構並未被數學家們所認識,直到19世紀末20世紀初,人們才把空間的性質與向量運算聯繫起來,使向量成為具有一套優良運算通性的數學體系。
向量能夠進入數學並得到發展,首先應從
複數 的幾何表示談起。18世紀末期,
挪威 測量學家威塞爾首次利用坐標平面上的點來表示複數
a +
b i(a,b為有理數,且不同時等於0),並利用具有幾何意義的複數運算來定義向量的運算。把坐標平面上的點用向量表示出來,並把向量的幾何表示用於研究幾何問題與三角問題。人們逐步接受了複數,也學會了利用複數來表示和研究平面中的向量,向量就這樣平靜地進入了數學中。
但
複數 的利用是受限制的,因為它僅能用於表示平面,若有不在同一平面上的力作用於同一物體,則需要尋找所謂
三維 “複數”以及相應的運算體系。19世紀中期,英國數學家
哈密爾頓 發明了
四元數 (包括數量部分和向量部分),以代表空間的向量。他的工作為向量代數和
向量分析 的建立奠定了基礎.隨後,
電磁理論 的發現者,英國的數學物理學家麥克斯韋把四元數的數量部分和向量部分分開處理,從而創造了大量的向量分析。
三維向量分析的開創,以及同四元數的正式分裂,是英國的居伯斯和海維塞德於19世紀80年代各自獨立完成的。他們提出,一個向量不過是四元數的向量部分,但不獨立於任何四元數。他們引進了兩種類型的
乘法 ,即
數量積 和
向量積 。並把向量
代數 推廣到變向量的向量
微積分 .從此,向量的
方法 被引進到分析和解析幾何中來,並逐步完善,成為了一套優良的
數學工具 。
表達方式
代數表示 一般印刷用黑體的小寫英文字母(
a 、
b 、
c 等)來表示,手寫用在a、b、c等字母上加一箭頭(
→ )表示,如
,也可以用大寫字母AB、CD上加一箭頭(
→ )等表示。
幾何表示 向量可以用
有向線段 來表示。有向
線段 的長度表示向量的大小,向量的大小,也就是向量的長度。長度為0的向量叫做
零向量 ,記作長度等於1個單位的向量,叫做
單位向量 。箭頭所指的方向表示向量的方向。
向量表示
坐標表示 在
平面直角坐標系 中,分別取與x軸、y軸方向相同的兩個單位向量
i ,
j 作為一組
基底 。a為平面直角坐標系內的任意向量,以坐標
原點 O為起點P為終點作向量a。由
平面向量基本定理 可知,有且只有一對
實數 (x,y),使得a=xi+yj,因此把實數對(x,y)叫做向量a的坐標,記作a=(x,y)。這就是向量a的坐標表示。其中(x,y)就是點
的坐標。向量a稱為點P的位置向量。
向量的坐標表示 在
空間直角坐標系 中,分別取與x軸、y軸,z軸方向相同的3個單位向量
i ,
j ,
k 作為一組
基底 。若為該
坐標系 內的任意向量,以坐標原點O為起點作向量a。由空間基本定理知,有且只有一組實數(x,y,z),使得a=ix+jy+kz,因此把實數對(x,y,z)叫做向量a的坐標,記作a=(x,y,z)。這就是向量a的坐標表示。其中(x,y,z),就是點P的坐標。向量a稱為點P的位置向量。
當然,對於多維的
空間向量 ,可以通過類推得到,此略。
向量的矩陣表示
行列式的幾何意義 行列式的值是一個數字,表示向量所在空間的【元素】 大小。
比如,在平面直角坐標系中,整個平面可以由長寬均為1的方格構成,這個方格的大小為1。這個方格就是平面直角坐標系中的【元素】,大小為1。
平面坐標系中所有的點都可以用
這兩個向量來刻畫,這兩個向量也叫平面直角坐標空間的【標度】。
這兩向量構成的行列式
那么,平面直角坐標系單元格大小,也就是【元素】大小為1的正方塊。
再比如,我們對平面直角坐標系拉伸,用如下兩個向量來刻畫
那么,這個新坐標系(2維空間)的【元素】大小為2的長方塊。
再比如,我們對平面直角坐標系變形,用如下兩個向量來刻畫
那么,這個新坐標系(2維空間)的【元素】大小為2的平行四邊形塊。
從以上3個例子,可以看出來:在2維空間中,兩個2維向量構成的的行列式的值,等同於兩個向量組成的平行四邊形面積大小。也就是說,在2維空間中,兩個2維向量構成的的行列式的值,等同於兩個2維向量的【叉積】。
進一步,看3維空間。
比如,在空間直角坐標系中,這個空間可以由長寬高均為1的正方體構成,這個正方體的大小為1。這個正方體就是空間直角坐標系(3維空間)中的【元素】,大小為1。
那么可以看出來:在3維空間中,三個3維向量構成的的行列式的值,等同於三個3維向量的【混合積】。
由此,擴展到n維空間。在n維空間中,n個n維向量構成的行列式的值,表示n維向量所在的n維空間的【元素】 大小。同時,這n個n維向量也叫n維空間的【標度】。
相關定義
有向線段 規定若線段
的
端點 為
起點 ,
為終點,則線段就具有了從起點
到終點
的方向和長度。
向量的模 向量的大小,也就是向量的長度(或稱模)。向量a的模記作|a|。
註:
1.向量的模是非負實數,向量的模是可以比較大小的。向量
,
。
2.
因為方向不能比較大小,所以向量也就不能比較大小。 對於向量來說“大於”和“小於”的概念是沒有意義的。例如
是沒有意義的。
單位向量 長度為一個單位(即模為1)的向量,叫做
單位向量 。與a同向,且長度為單位1的向量,叫做a方向上的單位向量,記作
。
負向量 如果向量AB與向量CD的模相等且方向相反,那么我們把向量AB叫做向量CD的
負向量 ,也稱為相反向量。
零向量 長度為0的向量叫做
零向量 ,記作
0 。零向量的始點和終點重合,所以零向量沒有確定的方向,或說零向量的方向是任意的。
相等向量 長度相等且方向相同的向量叫做
相等向量 .向量
a 與
b 相等,記作
a =
b 。
規定:所有的零向量都相等 。
當用有向線段表示向量時,起點可以任意選取。任意兩個相等的
非零向量 ,都可用同一條
有向線段 來表示,並且與有向線段的起點無關.同向且等長的有向線段都表示同一向量。
自由向量 始點不固定的向量,它可以任意的平行移動,而且移動後的向量仍然代表原來的向量。
向量 在自由向量的意義下,相等的向量都看作是同一個向量。
滑動向量
固定向量
位置向量 對於坐標平面內的任意一點P,我們把向量OP叫做點P的
位置向量 ,記作:向量
P 。
方向向量 直線l上的向量a以及與向量a共線的向量叫做直線l上的
方向向量 。
相反向量 與a長度相等、方向相反的向量叫做
a 的
相反向量 ,記作-
a ,有 -(-
a) =
a, 零向量 的相反向量仍是零向量。
平行向量 方向相同或相反的非零向量叫做平行(或共線)向量.向量a、b平行(共線),記作
a ∥
b 。零向量長度為零,是起點與終點重合的向量,其方向不確定。我們規定:零向量與任一向量平行。平行於同一直線的一組向量是
共線向量 。
若a =(x,y),b =(m,n),則a //b→ a ×b =xn-ym=0
共面向量 平行於同一平面的三個(或多於三個)向量叫做共面向量。
空間中的向量有且只有以下兩種位置關係:⑴共面;⑵不共面。
注意:只有三個或三個以上向量才談共面不共面。
法向量 直線l⊥α,取直線l的方向向量a,則向量a叫做平面α的
法向量 。
法向量 向量的和的模 設平面直角坐標系xOy中,有點A(x1 ,y1 )、B(x2 ,y2 ),則
運算
加法 向量的加法滿足平行四邊形法則和三角形法則,
。
向量的加法 交換律:a +b =b +a;
結合律:(a +b )+c =a +(b +c )。
減法 如果a 、b 是互為相反的向量,那么a =-b ,b =-a ,a +b =0. 0 的反向量為0
OA -
OB =
BA. 即“共同起點,指向被減”
向量的減法 a =(x1 ,y1 ),b =(x2 ,y2 ) ,則a -b =(x1 -x2 ,y1 -y2 ).
如圖:c=a-b 以b 的結束為起點,a 的結束為終點。
加減變換律:a +(-b )=a -b
數乘 實數λ和向量a的叉乘乘積是一個向量 ,記作λa ,且|λa |=|λ|* |a |。
當λ>0時,λa的方向與a的方向相同 ;當λ<0時,λa的方向與a的方向相反 ;當λ=0時,λa =0 ,方向任意。當a =0 時,對於任意實數λ,都有λa =0 。
註:按定義知,如果λa =0 ,那么λ=0或a =0 。
實數λ叫做向量
a 的
係數 ,乘數向量λ
a 的幾何意義就是將表示向量
a 的有向線段伸長或壓縮。
當 |λ| >1時,表示向量a 的有向線段在原方向(λ>0)或反方向(λ<0)上伸長為原來的|λ|倍
當|λ|<1時,表示向量a 的有向線段在原方向(λ>0)或反方向(λ<0)上縮短為原來的 |λ|倍。
實數p和向量a的點乘乘積是一個數。
數與向量的乘法滿足下面的運算律
結合律:(λa )·b =λ(a ·b )=(a ·λb )。
向量對於數的分配律(第一分配律):(λ+μ)a =λa +μa.
數對於向量的分配律(第二分配律):λ(a +b )=λa +λb.
數乘向量的消去律:① 如果實數λ≠0且λa= λb ,那么a=b 。② 如果a ≠0 且λa= μa ,那么λ= μ。
需要注意的是:向量的加減乘(向量沒有除法)運算滿足實數加減乘運算法則。
數量積 定義:已知兩個非零向量
a,b ,作
OA=a,OB=b ,則∠AOB稱作向量
a 和向量
b 的
夾角 ,記作
θ 並規定0≤
θ ≤π
定義:兩個向量的
數量積 (
內積 、
點積 )是一個數量(沒有方向),記作
a·b 。
向量的數量積的坐標表示:a ·b =x·x'+y·y'。
向量的數量積的運算律
向量的數量積的性質
a ⊥b 〈=〉a ·b =0。
|a ·b |≤|a |·|b |。(該公式證明如下:|a ·b |=|a |·|b |·|cosα| 因為0≤|cosα|≤1,所以|a ·b |≤|a |·|b |)
向量的數量積與實數運算的主要不同點
1.向量的數量積不滿足結合律,即:(a ·b )·c ≠a ·(b ·c );例如:(a ·b )2 ≠a2 ·b2 。
2.向量的數量積不滿足消去律,即:由a ·b =a ·c (a ≠0 ),推不出b =c 。
3.|a ·b |與|a |·|b |不等價
4.由 |a |=|b | ,不能推出a=b ,也不能推出a= -b ,但反過來則成立。
向量積 定義:兩個向量
a 和
b 的
向量積 (外積、
叉積 )是一個向量,記作
a ×
b(這裡“×”並不是乘號,只是一種表示方法,與“·”不同,也可記做“∧”) 。若
a 、
b 不共線,則
a ×
b 的模是:∣
a ×
b ∣=|
a |·|
b |·sin〈
a ,
b 〉;
a ×
b 的方向是:垂直於
a 和
b ,且
a 、
b 和
a ×
b 按這個次序構成
右手系 。若
a 、
b 垂直,則
∣a ×
b∣=|a|*|b|(此處與數量積不同,請注意),若a ×b =0 ,則a 、b 平行 。向量積即兩個不共線非零向量所在平面的一組法向量。
向量的幾何表示 運算法則:運用三階行列式
設a,b,c 分別為沿x,y,z軸的單位向量
A=(x1,y1,z1),B=(x2,y2,z2),則
向量的向量積性質:
|a ×b |是以a 和b 為邊的平行四邊形面積。
a ×a =0 。
a平行 b 〈=〉a ×b =0
向量的向量積運算律
a ×b =-b ×a
(λa )×b =λ(a ×b) =a ×(λb )
a ×(b+ c )=a ×b +a ×c.
(a +b )×c=a ×c +b ×c.
上兩個分配律分別稱為左分配律和右分配律。在演算中應注意不能交換“×”號兩側向量的次序。
注 :向量沒有除法,“向量AB/向量CD”是沒有意義的。
三向量混合積 定義:給定空間三向量
a 、
b 、
c ,向量
a 、
b 的向量積
a ×
b ,再和向量
c 作數量積(
a ×
b )·
c ,所得的數叫做三向量
a 、
b 、
c 的混合積,記作(
a ,
b ,
c )或(
a b c ),即(
a b c )=(
a ,
b ,
c )=(
a ×
b )·
c 向量的混合積 混合積具有下列性質:
1.三個不共面向量
a 、
b 、
c 的混合積的絕對值等於以
a 、
b 、
c 為棱的平行六面體的體積V,並且當
a 、
b 、
c 構成右手系時混合積是
正數 ;當
a 、
b 、
c 構成左手系時,混合積是
負數 ,即(
a b c )=εV(當
a 、
b 、
c 構成
右手系 時ε=1;當
a 、
b 、
c 構成左手系時ε=-1)
2.上性質的推論:三向量
a 、
b 、
c 共面的
充要條件 是(
a b c )=0
3.(a b c )=(b ca )=(cab )=-(ba c )=-(cba )=-(acb )
雙重向量積 給定空間的三個向量a ,b ,c ,如果先做其中兩個向量a ,b 的向量積a ×b ,再做所得向量與第三向量的向量積,那么最後的結果仍然是一個向量,叫做所給三向量的雙重向量積,記做:(a ×b )×c 。
性質:
(a ×b )×c =(a ·c )·b -(b ·c )·a
a ×(b ×c )=-(b ×c )×a =(a ·c )·b -(a ·b )·c
關係式 給定空間內四個向量a 、b 、c 、d ,則這四個向量之間滿足如下關係:
由混合積的性質可知
(即把
c ×
d 看成一個新的向量
e ,利用性質(
a ×
b )·
e=a ·(
b ×
e ))
再根據二重向量積的性質可知
證明 :令公式中a =c 、b =d ,則:
兩個向量構成的平行四邊形的面積公式
向量定理
共線定理 若
b ≠
0 ,則
a //
b 的充要條件是存在唯一
實數 λ,使
。若設
a =(x
1 ,y
1 ),
b =(x
2 ,y
2 ) ,則有
,與平行概念相同。
平行於任何向量。
垂直定理 a ⊥b 的充要條件是a·b =0, 即(x1 x2 +y1 y2 )=0 。
分解定理 平面向量分解定理:如果
、
是同一平面內的兩個不平行向量,那么對於這一平面內的任一向量,有且只有一對實數
,使
,我們把不平行向量
、
叫做這一平面內所有向量的
基底 。
定比分點公式 三點共線定理 已知O是AB所在直線外一點,若
, 且
則A、B、C三點共線
重心判斷式 垂心判斷式 內心判斷式 外心判斷式
向量空間
定義
同構 給定域F上的兩個向量空間V與V' ,如果存在一個
雙射 φ:V→V',並且
,
,
。這樣V與V' 便是
同構 的。
映射 給兩個向量空間V和W在同一個F場,設定由V到W的線性變換或“
線性映射 ” ,這些由V到W的映射都有共同點就是它們保持總和及
標量 商數。這個
集合 包含所有由V到W的
線性 映像,以 L(V,W) 來描述,也是一個F場裡的向量空間。當V及W被確定後,線性映射可以用
矩陣 來表達。同構是一對一的一張線性映射。如果在V 和W之間存在同構, 我們稱這兩個空間為同構。一個在F場的向量空間加上線性映像就可以構成一個
範疇 ,即
阿貝爾範疇 。
延伸 研究向量
空間 一般會涉及一些額外結構。額外結構如下:
一個實數或複數向量空間加上長度和角度的概念,稱為
內積空間 。
一個向量空間加上雙線性運算元(定義為向量乘法)是個域代數。
子空間及基 一個向量空間V的一個非空
子集 合W在加法及標量乘法中表現密閉性,被稱為V的線性子空間。給出一個向量
集 合B,那么包含它的最小子空間就稱為它的擴張,記作span(B)。給出一個向量集合B,若它的擴張就是向量空間V, 則稱B為V的生成集。一個向量空間V最大的
線性獨立 子集,稱為這個空間的基。若V=0,唯一的基是
空集 。對非零向量空間 V,基是 V 最小的生成集。如果一個向量空間 V 擁有一個元素個數有限的生成集,那么就稱V是一個有限
維空間 。向量空間的所有基擁有相同基數,稱為該空間的
維度 。例如,實數向量空間:
中,
的維度就是n。空間內的每個向量都有唯一的方法表達成基中元素的
線性組合 。把基中元素排列,向量便可以坐標系統來呈現。
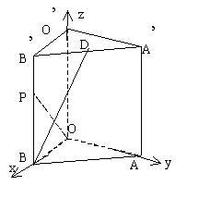 向量
向量

 向量的坐標表示
向量的坐標表示









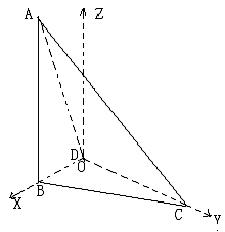 向量
向量 法向量
法向量



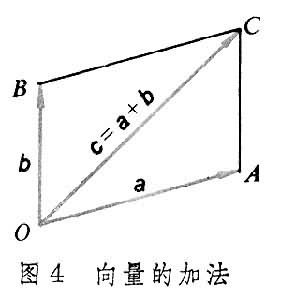 向量的加法
向量的加法
 向量的減法
向量的減法


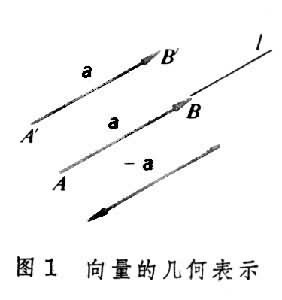 向量的幾何表示
向量的幾何表示
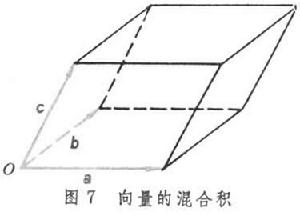 向量的混合積
向量的混合積


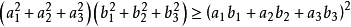



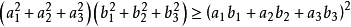

















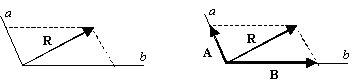 向量表示
向量表示














