基本介紹
- 中文名:行向量
- 外文名:row vector
- 適用範圍:數理科學
定義
符號
 圖1.行向量的轉置
圖1.行向量的轉置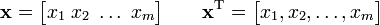 圖2.行向量的表示
圖2.行向量的表示矩陣
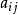


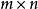
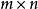
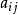





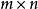

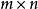

 圖1.行向量的轉置
圖1.行向量的轉置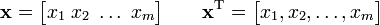 圖2.行向量的表示
圖2.行向量的表示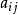


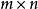
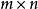
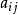





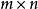

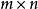
線上性代數中,行向量是一個 1×n的矩陣,即矩陣由一個含有n個元素的行所組成即行向量。行向量的轉置是一個列向量,反之亦然。所有的行向量的集合形成一個向量...
線上性代數中,列向量是一個 n×1 的矩陣,即矩陣由一個含有n個元素的列所組成:列向量的轉置是一個行向量,反之亦然。所有的列向量的集合形成一個向量空間,它...
向量處理器,又稱數組處理器,是一種實現了直接操作一維數組(向量)指令集的中央處理器(CPU)。...
線上性代數中,行向量或行矩陣是1×m階矩陣,即由單行m個元素組成的矩陣,記作A=(a1 a2…am),為避免元素間的混淆,也記作A=(a1,a2,…an)。...
logspace是一個MATLAB類型的函式,相關函式是linspace。其功能是行向量,生成從10的a次方到10的b次方之間按對數等分的n個元素的行向量。n如果省略,則默認值為50。在...
功能:從系統矩陣中選擇輸入和輸出量,並從變矩陣中選擇行向量、列向量值。字元‘:’代表選擇所有的行、列向量。在matlab的命令視窗中輸入help sel可以獲得更多幫助信...
列矩陣又稱列向量,是指有一列的矩陣。如果矩陣 A=(aij)m×n只有一行,即m=1,則此時稱之為行矩陣,或行向量。同樣,若 A=(aij)m×n只有一列,即n=1,這時...
對於任一向量組而言,,不是線性無關的就是線性相關的。 向量組只包含一個向量a時,a為0向量,則說A線性相關; 若a≠0, 則說A線性無關。 包含零向量的任何...
類似地,行秩是A的線性無關的橫行的極大數目。即如果把矩陣看成一個個行向量或者列向量,秩就是這些行向量或者列向量的秩,也就是極大無關組中所含向量的個數...
MIMD類的機器又可分為以下常見的五類:並行向量處理機(PVP)、對稱多處理機(SMP...需要使用者有較高的專業素質,多數是命令行的操作,這是很多專業人士的噩夢,更不...
數學上,任一的MxN離散線性轉換皆可表示成矩陣(Matrix) 的型式:Y=AX,再進一步假設,若矩陣Aby正交基底 (Orthogonal basis) 列向量(Row vector) 所組成,也可表示...
對於線性規劃問題:min cTx,s.t.Ax=b,x≥0,其中m≤n,且m×n矩陣A的秩為m。由矩陣A的m個線性無關的列向量組成的m階方陣,記為B,稱之為基。一個基相應...
其中R是產品部門淨產值與折舊之和的n維列向量,X是總產品n維列向量,1是n階單位陣,表示投人產品消耗係數對角陣,a;;(i, j=1,2,w,n)是直接消耗係數.實物型...
線性代數數據元多個向量集成的向量組可構造矩陣,方陣的行列式是求矩陣的數量。三個數據元的表示方法是多樣的。...
