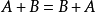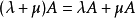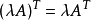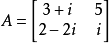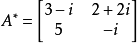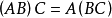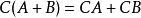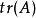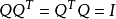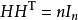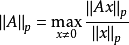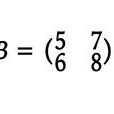歷史 在數學中,矩陣(Matrix)是一個按照長方陣列排列的
複數 或
實數 集合,最早來自於
方程組 的
係數 及
常數 所構成的
方陣 。這一概念由19世紀英國數學家
凱利 首先提出。作為解決
線性方程 的工具,矩陣也有不短的歷史。成書最早在東漢前期的《
九章算術 》中,用分離
係數 法表示
線性方程組 ,得到了其
增廣矩陣 。在
消元 過程中,使用的把某行乘以某一非零
實數 、從某行中減去另一行等運算技巧,相當於矩陣的
初等變換 。但那時並沒有現今理解的矩陣概念,雖然它與現有的矩陣形式上相同,但在當時只是作為線性方程組的標準表示與處理方式。
阿瑟·凱利,矩陣論奠基人 矩陣的概念在19世紀逐漸形成。1800年代,
高斯 和威廉·若爾當建立了高斯—若爾當消去法。1844年,
德國 數學家
費迪南·艾森斯坦 (F.Eisenstein)討論了“變換”(矩陣)及其乘積。1850年,英國數學家
詹姆斯·約瑟夫·西爾維斯特 (James Joseph Sylvester)首先使用矩陣一詞。
詹姆斯約瑟夫西爾維斯特 英國
數學家 阿瑟·凱利被公認為矩陣論的
奠基人 。他開始將矩陣作為獨立的
數學 對象研究時,許多與矩陣有關的性質已經在行列式的研究中被發現了,這也使得凱利認為矩陣的引進是十分自然的。他說:“我決然不是通過
四元數 而獲得矩陣概念的;它或是直接從行列式的概念而來,或是作為一個表達線性方程組的方便方法而來的。”他從1858年開始,發表了《矩陣論的研究報告》等一系列關於矩陣的專門論文,研究了矩陣的運算律、矩陣的逆以及
轉置 和
特徵多項式 方程。
凱利 還提出了凱萊-哈密爾頓定理,並驗證了3×3矩陣的情況,又說進一步的證明是不必要的。
哈密爾頓 證明了4×4矩陣的情況,而一般情況下的證明是德國數學家
弗羅貝尼烏斯 (F.G.Frohenius)於1898年給出的。
1854年時
法國 數學家
埃爾米特 (C.Hermite)使用了“
正交矩陣 ”這一術語,但他的正式定義直到1878年才由費羅貝尼烏斯發表。1879年,費羅貝尼烏斯引入矩陣
秩 的概念。至此,矩陣的體系基本上建立起來了。
無限維矩陣的研究始於1884年。
龐加萊 在兩篇不嚴謹地使用了無限維矩陣和行列式理論的文章後開始了對這一方面的專門研究。1906年,
希爾伯特 引入無限二次型(相當於無限維矩陣)對積分方程進行研究,極大地促進了無限維矩陣的研究。在此基礎上,
施密茨 、赫林格和特普利茨發展出運算元理論,而無限維矩陣成為了研究
函式 空間運算元的有力工具。
矩陣的
概念 最早在1922年見於中文。1922年,程廷熙在一篇介紹文章中將矩陣譯為“縱橫陣”。1925年,科學名詞審查會算學名詞審查組在《
科學 》第十卷第四期刊登的審定名詞表中,矩陣被翻譯為“矩陣式”,
方塊矩陣 翻譯為“方陣式”,而各類矩陣如“正交矩陣”、“
伴隨矩陣 ”中的“矩陣”則被翻譯為“方陣”。1935年,
中國數學會 審查後,
中華民國教育部 審定的《數學名詞》(並“通令全國各院校一律遵用,以昭劃一”)中,“矩陣”作為譯名首次出現。1938年,曹惠群在接受科學名詞審查會委託就
數學名詞 加以校訂的《算學名辭彙編》中,認為應當的譯名是“長方陣”。中華人民共和國成立後編訂的《
數學名詞 》中,則將譯名定為“(矩)陣”。1993年,中國自然科學名詞審定委員會公布的《
數學名詞 》中,“矩陣”被定為正式譯名,並沿用至今。
定義 由 m × n 個數aij 排成的m行n列的數表稱為m行n列的矩陣,簡稱m × n矩陣。記作:
這m×n 個數稱為矩陣A ij 位於矩陣A A ij 為(i,j)元的矩陣可記為(aij )或(aij )m × n ,m×n矩陣A Amn
元素是
實數 的矩陣稱為
實矩陣 ,元素是
複數 的矩陣稱為
復矩陣 。而行數與列數都等於n的矩陣稱為n階矩陣或n階方陣。
基本運算 矩陣運算在
科學計算 中非常重要,而矩陣的基本運算包括矩陣的加法,減法,數乘,轉置,共軛和共軛轉置。
加法 矩陣的加法滿足下列運算律(A ,B ,C 都是同型矩陣):
應該注意的是只有同型矩陣之間才可以進行加法。
減法
數乘 矩陣的數乘滿足以下運算律:
矩陣的加減法和矩陣的數乘合稱矩陣的線性運算。
轉置 把矩陣A的行和列互相交換所產生的矩陣稱為A的轉置矩陣,這一過程稱為矩陣的轉置
共軛 矩陣的共軛定義為:
.一個2×2複數矩陣的共軛如下所示:
則
共軛轉置 矩陣的共軛轉置定義為:
,也可以寫為:
。一個2×2複數矩陣的共軛如下所示:
乘法 兩個矩陣的乘法僅當第一個矩陣
A 的列數和另一個矩陣
B 的行數相等時才能定義。如
A 是
m ×
n 矩陣和
B 是
n ×
p 矩陣,它們的乘積
C 是一個
m ×
p 矩陣
,它的一個元素:
例如:
矩陣的乘法滿足以下運算律:
行列式 一個
n ×
n 的正方矩陣
A 的行列式記為
或者
, 一個2×2矩陣的行列式可表示如下:
一個n×n矩陣的行列式等於其任意行(或列)的元素與對應的
代數餘子式 乘積之和,即:
特徵值與特徵向量 n ×
n 的方塊矩陣
A 的一個特徵值和對應特徵向量是滿足
的
標量 以及非零向量。其中
v 為特徵向量
, 為特徵值。
A 的所有特徵值的全體,叫做A的譜,記為
。矩陣的特徵值和特徵向量可以揭示線性變換的深層特性。
矩陣的跡 矩陣A的對角元素之和稱為矩陣A的跡(trace),記作
, 即
正定性 n ×
n 的實對稱矩陣
A 如果滿足對所有非零向量
,對應的
二次型 若
,就稱
A 為正定矩陣。若
則
A 是一個
負定矩陣 ,若
,則
A 為
半正定矩陣 ,若
A 既非半正定,也非半負定,則
A 為
不定矩陣 。對稱矩陣的正定性與其特徵值密切相關。矩陣是正定的若且唯若其
特徵 值都是正數。
矩陣的分解 矩陣分解是將一個矩陣分解為比較簡單的或具有某種特性的若干矩陣的和或乘積,矩陣的分解法一般有三角分解、譜分解、
奇異值分解 、滿秩分解等。
三角分解 設
,則A可以唯一地分解為
A =
U 1 R , 其中
U1 是酉矩陣
,R 是正線上三角復矩陣
, 或
A 可以唯一地分解為其中
L 是正線上三角復矩陣
, 是酉矩陣
。 譜分解 譜分解(Spectral decomposition)是將
矩陣 分解為由其
特徵值 和
特徵向量 表示的矩陣之積的方法。需要注意只有對
可對角化矩陣 才可以施以特徵分解。
奇異值分解 假設
M 是一個
m×n 階
矩陣 ,其中的元素全部屬於
域 K ,也就是
實數 域或
複數 域。如此則存在一個分解使得
其中
U 是
m×m 階
酉矩陣 ;Σ是
m×n 階
實數 對角矩陣 ;而
V* ,即
V 的
共軛轉置 ,是
n×n 階酉矩陣。這樣的分解就稱作
M 的奇異值分解。Σ對角線上的元素Σ
i ,i 即為
M 的
奇異值 。常見的做法是將奇異值由大而小排列。如此Σ便能由
M 唯一確定了。
滿秩分解 設
,若存在矩陣
及
, 使得
A =
FG , 則稱其為的
A 一個滿秩分解。
LUP分解 LUP 分解的思想就是找出三個
n×n 矩陣
L ,U ,P ,滿足
. 其中L是一個單位下三角矩陣,U是一個單位上三角矩陣,P是一個置換矩陣。 而滿足分解條件的矩陣
L ,
U ,
P 稱為矩陣A的一個
LUP 分解。
特殊類別
對稱矩陣 在
線性代數 中,對稱矩陣是一個方形矩陣,其轉置矩陣和自身相等。即
.例如:
.
Hermitian矩陣 一個正方的復值矩陣
稱為Hermitian矩陣,若
A =
AH 即其元素
,換言之Hermitian矩陣是一種復共軛對稱矩陣。
對一個實值矩陣,Hermitian矩陣與對稱矩陣等價。
正交矩陣
酉矩陣
帶型矩陣 矩陣
,若矩陣滿足條件a
ij =0,|i-j|>k,則矩陣
A 可以稱為帶型矩陣(banded matrix)。
三角矩陣 在
線性代數 中,三角矩陣是方形矩陣的一種,因其非零係數的排列呈三角形狀而得名。三角矩陣分上三角矩陣和下三角矩陣兩種。若
,則
的矩陣稱為上三角矩陣,若
,則
的矩陣稱為下三角矩陣。三角矩陣可以看做是一般方陣的一種簡化情形。
相似矩陣 相合矩陣 令
,並且
C 非奇異,則矩陣
稱為
A 的相合矩陣。其中線性變換
稱為相合變換。
Vandermonde矩陣 Vandermonde矩陣(范德蒙矩陣)的命名來自Alexandre-Théophile Vandermonde的名字,范德蒙矩陣是一個各列呈現出
幾何級數 關係的
矩陣 。
例如:
Hadamard矩陣 Hadamard矩陣(阿達馬矩陣)是一個
方陣 ,每個元素都是 +1 或 −1,每行都是互相正交的。
n 階的阿達馬矩陣
H 滿足:
。這裡
In 是
n ×
n 的
單位矩陣 。
對角矩陣 對於
m×m 的矩陣,當
時,有
,此時所有非對角線上的元素均為0,此時的矩陣稱為對角矩陣。
分塊矩陣 一個分塊矩陣是將矩陣分割出較小的矩陣,這些較小的矩陣就稱為子塊。例如:
該矩陣可以分為四個2×2 的矩陣:
分塊後的矩陣可以寫為如下形式:
Jacobian矩陣 Jacobian矩陣是函式的一階
偏導數 以一定方式排列成的矩陣。
可表示為如下形式:
旋轉矩陣(Rotation matrix) 旋轉矩陣(Rotation matrix)是在乘以一個向量的時候有改變向量的方向但不改變大小的效果的矩陣。旋轉矩陣不包括反演,它可以把右手坐標系改變成左手坐標系或反之。所有旋轉加上反演形成了正交矩陣的集合。
旋轉矩陣是世界上著名的彩票專家、澳大利亞數學家底特羅夫研究的,它可以幫助您鎖定喜愛的號碼,提高中獎的機會。首先您要先選一些號碼,然後,運用某一種旋轉矩陣,將你挑選的數字填入相應位置。如果您選擇的數字中有一些與開獎號碼一樣,您將一定會中一定獎級的獎。當然運用這種旋轉矩陣,可以最小的成本獲得最大的收益,且遠遠小於複式投注的成本。
旋轉矩陣的原理在數學上涉及到的是一種組合設計:覆蓋設計。而覆蓋設計,填裝設計,斯坦納系,t-設計都是離散數學中的組合最佳化問題。它們解決的是如何組合集合中的元素以達到某種特定的要求。
範數 矩陣的範數主要包括三種主要類型:誘導範數,元素形式範數和Schatten範數。
誘導範數 誘導範數又稱
矩陣空間上的
運算元範數 (operator norm),定義為:
常用的誘導範數為p-範數:
p範數也稱為明克夫斯基 p範數或者
範數。特別的,當
時,對應的誘導範數分別為
元素形式範數 將
矩陣按照列的形式,排成一個
的向量,然後採用向量範數的定義,即得到矩陣的元素形式範數,表式如下:
Schatten範數 Schatten範數是用矩陣的
奇異值 定義的範數,定義為:
套用
圖像處理 在圖像處理中圖像的仿射變換一般可以表示為一個仿射矩陣和一張原始圖像相乘的形式,例如,
這裡表示的是一次線性變換再接上一個平移。
線性變換及對稱 線性變換及其所對應的
對稱 ,在現代
物理學 中有著重要的角色。例如,在
量子場論 中,
基本粒子 是由狹義相對論的
洛倫茲群 所表示,具體來說,即它們在旋量群下的表現。內含
泡利矩陣 及更通用的
狄拉克矩陣 的具體表示,在
費米子 的物理描述中,是一項不可或缺的構成部分,而費米子的表現可以用
旋量 來表述。描述最輕的三種
夸克 時,需要用到一種內含
特殊酉群 SU(3)的群論表示;物理學家在計算時會用一種更簡便的矩陣表示,叫
蓋爾曼矩陣 ,這種矩陣也被用作SU(3)規範群,而強核力的現代描述──
量子色動力學 的基礎正是SU(3)。還有
卡比博-小林-益川矩陣 (CKM矩陣):在
弱相互作用 中重要的基本夸克態,與指定粒子間不同質量的夸克態不一樣,但兩者卻是成線性關係,而CKM矩陣所表達的就是這一點。
量子態的線性組合 1925年海森堡提出第一個
量子力學 模型時,使用了無限維矩陣來表示理論中作用在量子態上的運算元。這種做法在
矩陣力學 中也能見到。例如
密度矩陣 就是用來刻畫量子系統中“純”
量子態 的線性組合表示的“混合”量子態。
另一種矩陣是用來描述構成實驗粒子物理基石的散射實驗的重要工具。當粒子在
加速器 中發生碰撞,原本沒有相互作用的粒子在高速運動中進入其它粒子的作用區,動量改變,形成一系列新的粒子。這種碰撞可以解釋為結果粒子狀態和入射粒子狀態線性組合的標量積。其中的線性組合可以表達為一個矩陣,稱為
S矩陣 ,其中記錄了所有可能的粒子間相互作用。
簡正模式 矩陣在物理學中的另一類泛套用是描述線性耦合調和系統。這類系統的
運動方程 可以用矩陣的形式來表示,即用一個質量矩陣乘以一個廣義速度來給出運動項,用力矩陣乘以位移向量來刻畫相互作用。求系統的解的最優方法是將矩陣的特徵向量求出(通過
對角化 等方式),稱為系統的簡正模式。這種求解方式在研究分子內部動力學模式時十分重要:系統內部由化學鍵結合的原子的振動可以表示成簡正振動模式的疊加。描述力學振動或電路振盪時,也需要使用簡正模式求解。
幾何光學 在
幾何光學 里,可以找到很多需要用到矩陣的地方。幾何光學是一種忽略了光波波動性的近似理論,這理論的模型將光線視為幾何
射線 。採用近軸近似(英語:paraxial approximation),假若光線與光軸之間的夾角很小,則
透鏡 或反射元件對於光線的作用,可以表達為2×2矩陣與向量的乘積。這向量的兩個分量是光線的幾何性質(光線的
斜率 、光線跟光軸之間在
主平面 (英語:principal plane)的垂直距離)。這矩陣稱為
光線傳輸矩陣 (英語:ray transfer matrix),內中元素編碼了光學元件的性質。對於折射,這矩陣又細分為兩種:“折射矩陣”與“平移矩陣”。折射矩陣描述光線遇到透鏡的折射行為。平移矩陣描述光線從一個主平面傳播到另一個主平面的平移行為。
由一系列
透鏡 或反射元件組成的光學系統,可以很簡單地以對應的矩陣組合來描述其光線傳播路徑。
電子學 在
電子學 里,傳統的網目分析(英語:mesh analysis)或節點分析會獲得一個
線性方程組 ,這可以以矩陣來表示與計算。
 阿瑟·凱利,矩陣論奠基人
阿瑟·凱利,矩陣論奠基人 詹姆斯約瑟夫西爾維斯特
詹姆斯約瑟夫西爾維斯特