學科簡史,基本原理,狀態函式,微觀體系,玻爾理論,泡利原理,歷史背景,黑體輻射問題,光電效應實驗,原子光譜學,光量子理論,德布羅意波,量子物理學,實驗現象,光電效應,原子能級躍遷,電子的波動性,相關概念,波和粒子,測量過程,不確定性,理論演變,套用學科,原子物理學,固體物理學,量子信息學,量子力學解釋,量子力學問題,解釋,
學科簡史
量子力學是描寫原子和
亞原子尺度的
物理學理論。該理論形成於20世紀初期,徹底改變了人們對物質組成成分的認識。微觀世界裡,粒子不是檯球,而是嗡嗡跳躍的
機率雲,它們不只存在一個位置,也不會從點A通過一條單一路逕到達點B。根據量子理論,粒子的行為常常像
波,用於描述粒子行為的“波函式”預測一個粒子可能的特性,諸如它的位置和速度,而非確定的特性。物理學中有些怪異的概念,諸如糾纏和
不確定性原理,就源於量子力學。
量子力學的發展革命性地改變了人們對物質的結構以及其相互作用的認識。量子力學得以解釋許多現象和預言新的、無法直接想像出來的現象,這些現象後來也被非常精確的實驗證明。除通過
廣義相對論描寫的引力外,至今所有其它物理
基本相互作用均可以在量子力學的框架內描寫(
量子場論)。
量子力學並沒有支持
自由意志,只是於微觀世界物質具有
機率波等存在
不確定性,不過其依然具有穩定的
客觀規律,不以人的意志為轉移,否認
宿命論。第一,這種微觀尺度上的隨機性和通常意義下的巨觀尺度之間仍然有著難以逾越的距離;第二,這種隨機性是否不可約簡難以證明,事物是由各自獨立演化所組合的多樣性整體,
偶然性與
必然性存在
辯證關係。自然界是否真有隨機性還是一個懸而未決的問題,對這個鴻溝起決定作用的就是
普朗克常數,統計學中的許多
隨機事件的例子,嚴格說來實為決定性的。
在量子力學中,一個物理體系的狀態由
波函式表示,波函式的任意
線性疊加仍然代表體系的一種可能狀態。對應於代表該量的
算符對其波函式的作用;波函式的模平方代表作為其變數的
物理量出現的
幾率密度。
1905年,愛因斯坦引進
光量子(
光子)的概念,並給出了光子的能量、
動量與輻射的頻率和波長的關係,成功地解釋了
光電效應。其後,他又提出固體的振動能量也是
量子化的,從而解釋了低溫下
固體比熱問題。
1913年,玻爾在
盧瑟福原有核原子模型的基礎上建立起原子的量子理論。按照這個理論,原子中的電子只能在分立的軌道上運動,在軌道上運動時候電子既不吸收能量,也不放出能量。原子具有確定的能量,它所處的這種狀態叫“
定態”,而且原子只有從一個定態到另一個定態,才能吸收或輻射能量。這個理論雖然有許多成功之處,對於進一步解釋實驗現象還有許多困難。
 普朗克
普朗克在人們認識到光具有波動和微粒的二象性之後,為了解釋一些經典理論無法解釋的現象,法國物理學家
德布羅意於1923年提出了
物質波這一概念。認為一切微觀粒子均伴隨著一個波,這就是所謂的
德布羅意波。
德布羅意的物質波方程:
,
,其中
,可以由
得到
。
由於微觀粒子具有
波粒二象性,微觀粒子所遵循的運動規律就不同於巨觀物體的運動規律,描述微觀粒子運動規律的量子力學也就不同於描述巨觀物體運動規律的
經典力學。當粒子的大小由微觀過渡到巨觀時,它所遵循的規律也由量子力學過渡到經典力學。
1925年,海森堡基於物理理論只處理可觀察量的認識,拋棄了不可觀察的軌道概念,並從可觀察的輻射頻率及其強度出發,和
玻恩、
約爾當一起建立起
矩陣力學;1926年,薛丁格基於量子性是微觀體系波動性的反映這一認識,找到了微觀體系的運動方程,從而建立起
波動力學,其後不久還證明了波動力學和
矩陣力學的數學等價性;狄拉克和約爾丹各自獨立地發展了一種普遍的變換理論,給出量子力學簡潔、完善的數學表達形式。
 波粒二象性
波粒二象性當微觀粒子處於某一狀態時,它的力學量(如坐標、動量、
角動量、能量等)一般不具有確定的數值,而具有一系列可能值,每個可能值以一定的幾率出現。當粒子所處的狀態確定時,力學量具有某一可能值的幾率也就完全確定。這就是1927年,
海森伯得出的
測不準關係,同時玻爾提出了
並協原理,對量子力學給出了進一步的闡釋。
海森堡還提出了
測不準原理,原理的公式表達如下:
。
基本原理
量子力學基本的數學框架建立於:
量子態的描述和統計詮釋、
運動方程、觀測物理量之間的對應規則、測量公設、全同粒子公設的基礎上。
狀態函式
在量子力學中,一個物理體系的狀態由
狀態函式表示,狀態函式的任意線性疊加仍然代表體系的一種可能狀態。狀態隨時間的變化遵循一個
線性微分方程,該方程預言體系的行為,
物理量由滿足一定條件的、代表某種運算的
算符表示;測量處於某一狀態的物理體系的某一物理量的操作,對應於代表該量的算符對其狀態函式的作用;測量的可能取值由該算符的
本徵方程決定,測量的
期望值由一個包含該算符的
積分方程計算。 (一般而言,量子力學並不對一次觀測確定地預言一個單獨的結果。
 玻爾
玻爾取而代之,它預言一組可能發生的不同結果,並告訴我們每個結果出現的機率。也就是說,如果我們對大量類似的系統作同樣地測量,每一個系統以同樣的方式起始,我們將會找到測量的結果為A出現一定的次數,為B出現另一不同的次數等等。人們可以預言結果為A或B的出現的次數的近似值,但不能對個別測量的特定結果做出預言。)狀態函式的模平方代表作為其變數的物理量出現的幾率。根據這些基本原理並附以其他必要的假設,量子力學可以解釋原子和
亞原子的各種現象。
根據
狄拉克符號表示,狀態函式,用<Ψ|和|Ψ>表示,狀態函式的
機率密度用ρ=<Ψ|Ψ>表示,其機率流密度用(?/2mi)(Ψ*▽Ψ-Ψ▽Ψ*)表示,其機率為機率密度的空間積分。
狀態函式可以表示為展開在正交空間集裡的態矢比如
,其中|i>為彼此正交的空間基矢,
為狄拉克函式,滿足正交歸一性質。 態函式滿足
薛丁格波動方程,
,分離變數後就能得到不顯含時狀態下的演化方程
,En是能量
本徵值,H是
哈密頓運算元。
於是經典物理量的量子化問題就歸結為薛丁格波動方程的求解問題。
微觀體系
體系狀態
在量子力學中,體系的狀態有兩種變化,一種是體系的狀態按運動方程演進,這是可逆的變化;另一種是測量改變體系狀態的不可逆變化。因此,量子力學對決定狀態的物理量不能給出確定的預言,只能給出物理量取值的幾率。在這個意義上,
經典物理學因果律在微觀領域失效了。
據此,一些物理學家和哲學家斷言量子力學擯棄因果性,而另一些物理學家和哲學家則認為量子力學因果律反映的是一種新型的因果性——幾率因果性。量子力學中代表量子態的波函式是在整個空間定義的,態的任何變化是同時在整個空間實現的。
微觀體系
20世紀70年代以來,關於遠隔粒子關聯的實驗表明,類空分離的事件存在著量子力學預言的關聯。這種關聯是同
狹義相對論關於客體之間只能以不大於光速的速度傳遞物理相互作用的觀點相矛盾的。於是,有些物理學家和哲學家為了解釋這種關聯的存在,提出在
量子世界存在一種全局因果性或整體因果性,這種不同於建立在狹義相對論基礎上的局域因果性,可以從整體上同時決定相關體系的行為。
 量子力學
量子力學量子力學用
量子態的概念表征微觀體系狀態,深化了人們對物理實在的理解。微觀體系的性質總是在它們與其他體系,特別是觀察儀器的相互作用中表現出來。
人們對觀察結果用經典物理學語言描述時,發現微觀體系在不同的條件下,或主要表現為波動圖象,或主要表現為粒子行為。而量子態的概念所表達的,則是微觀體系與儀器相互作用而產生的表現為波或粒子的可 能性。
玻爾理論
玻爾,量子力學的傑出貢獻者,玻爾指出:電子軌道量子化概念。玻爾認為, 原子核具有一定的能級,當原子吸收能量,原子就
躍遷更高能級或
激發態,當原子放出能量,原子就躍遷至更低能級或基態,
原子能級是否發生躍遷,關鍵在兩能級之間的差值。根據這種理論,可從理論計算出里德伯常量,與實驗符合的相當好。
 電子云
電子云 可玻爾理論也具有局限性,對於較大原子,計算結果誤差就很大,玻爾還是保留了巨觀世界
中軌道的概念,其實電子在空間出現的坐標具有不確定性,電子聚集的多,就說明電子在這裡出現的機率較大,反之,機率較小。很多電子聚集在一起,可以形象的稱為
電子云。
泡利原理
由於從原則上,無法徹底確定一個量子物理系統的狀態,因此在量子力學中內在特性(比如質量、電荷等)完全相同的粒子之間的區分,失去了其意義。在經典力學中,每個粒子的位置和動量,全部是完全可知的,它們的軌跡可以被預言。通過一個測量,可以確定每一個粒子。在量子力學中,每個粒子的位置和動量是由
波函式表達,因此,當幾個粒子的波函式互相重疊時,給每個粒子“掛上一個標籤”的做法失去了其意義。
這個
全同粒子(identical particles) 的不可區分性,對狀態的
對稱性,以及多粒子系統的
統計力學,有深遠的影響。比如說,一個由全同粒子組成的多粒子系統的狀態,在交換兩個粒子“1”和粒子“2”時,我們可以證明,不是對稱的,即是反對稱的。對稱狀態的粒子是被稱為
玻色子,反對稱狀態的粒子是被稱為
費米子。此外
自旋的對換也形成對稱:自旋為半數的粒子(如電子、
質子和
中子)是反對稱的,因此是費米子;自旋為整數的粒子(如光子)是對稱的,因此是玻色子。
這個深奧的粒子的自旋、對稱和統計學之間關係,只有通過相對論量子場論才能導出,它也影響到了
非相對論量子力學中的現象。費米子的反對稱性的一個結果是
泡利不相容原理,即兩個費米子無法占據同一狀態。這個原理擁有極大的實用意義。它表示在我們的由原子組成的物質世界裡,電子無法同時占據同一狀態,因此在最低狀態被占據後,下一個電子必須占據次低的狀態,直到所有的狀態均被滿足為止。這個現象決定了物質的物理和化學特性。
歷史背景
19世紀末20世紀初,經典物理已經發展到了相當完善的地步,但在實驗方面又遇到了一些嚴重的困難,這些困難被看作是“晴朗天空的幾朵烏雲”,正是這幾朵烏雲引發了物理界的變革。下面簡述幾個困難:
黑體輻射問題
19世紀末,許多物理學家對
黑體輻射非常感興趣。
黑體是一個理想化了的物體,它可以吸收,所有照射到它上面的輻射,並將這些輻射轉化為熱輻射,這個熱輻射的光譜特徵僅與該黑體的溫度有關。使用經典物理這個關係無法被解釋。通過將物體中的原子看作微小的諧振子,
馬克斯·普朗克得以獲得了一個黑體輻射的
普朗克公式。但是在引導這個公式時,他不得不假設這些原子諧振子的能量,不是連續的(這與經典物理學的觀點相違背),而是離散的: En=nhν

這裡n是一個整數,h是一個自然常數。(後來證明正確的公式,應該以n+1/2來代替n,參見零點能量。)。1900年,普朗克在描述他的輻射能量子化的時候非常地小心,他僅假設被吸收和放射的輻射能是量子化的。今天這個新的自然常數被稱為
普朗克常數來紀念普朗克的貢獻。其值:
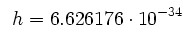 值
值光電效應實驗
由於紫外線照射,大量電子從金屬表面逸出。經研究發現,光電效應呈現以下幾個特點:
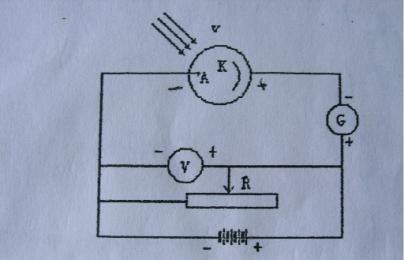 光電效應
光電效應a. 有一個確定的臨界頻率,只有入射光的頻率大於臨界頻率,才會有
光電子逸出。
b. 每個光電子的能量只與照射光的頻率有關。
c. 入射光頻率大於臨界頻率時,只要光一照上,幾乎立刻觀測到光電子。
以上3個特點,c是定量上的問題,而a、b在原則上無法用經典物理來解釋。
原子光譜學
光譜分析積累了相當豐富的資料,不少科學家對它們進行了整理與分析,發現
原子光譜是呈分立的線狀光譜而不是連續分布。譜線的波長也有一個很簡單的規律。
盧瑟福模型發現後,按照經典電動力學,加速運動的帶電粒子將不斷輻射而喪失能量。故,圍繞原子核運動的電子終會因大量喪失能量而’掉到’原子核中去。這樣原子也就崩潰了。現實世界表明,原子是穩定的存在著。
能量均分定理
光量子理論
量子理論是首先在
黑體輻射問題上突破的。普朗克為了從理論上推導他的公式,提出了量子的概念-h,不過在當時沒有引起很多人的注意。愛因斯坦利用量子假設提出了光量子的概念,從而解決了光電效應的問題。愛因斯坦還進一步把能量不連續的概念用到了固體中原子的振動上去,成功的解決了固體比熱在T→0K時趨於0的現象。光量子概念在康普頓散射實驗中得到了直接的驗證。
玻爾的量子論
玻爾把普朗克-愛因斯坦的概念創造性的用來解決原子結構和原子光譜的問題,提出了他的原子的量子論。主要包括兩個方面:
a. 原子能且只能穩定的存在分立的能量相對應的一系列的狀態中。這些狀態成為定態。
b. 原子在兩個定態之間躍遷時,吸收或發射的頻率v是唯一的,由hv=En-Em 給出。
玻爾的理論取得了很大的成功,首次打開了人們認識原子結構的大門,但是隨著人們對原子認識進一步加深,它存在的問題和局限性也逐漸為人們發現。
德布羅意波
在普朗克與愛因斯坦的光量子理論及玻爾的原子量子論的啟發下,考慮到光具有波粒二象性,德布羅意根據類比的原則,構想實物粒子也具有波粒二象性。他提出這個假設,一方面企圖把實物粒子與光統一起來,另一方面是為了更自然的去理解能量的不連續性,以克服玻爾量子化條件帶有人為性質的缺點。實物粒子波動性的直接證明,是在1927年的
電子衍射實驗中實現的。
量子物理學
量子力學本身是在1923-1927年一段時間中建立起來的。兩個等價的理論---矩陣力學和波動力學幾乎同時提出。矩陣力學的提出與玻爾的早期量子論有很密切的關係。海森堡一方面繼承了早期量子論中合理的核心,如能量量子化、定態、躍遷等概念,同時又摒棄了一些沒有實驗根據的概念,如電子軌道的概念。海森堡、玻恩和約爾丹的矩陣力學,從物理上可觀測量,賦予每一個物理量一個矩陣,它們的代數運算規則與經典物理量不同,遵守乘法不可易的代數。
波動力學來源於物質波的思想。薛丁格在物質波的啟發下,找到一個量子體系物質波的
運動方程-薛丁格方程,它是波動力學的核心。後來薛丁格還證明,矩陣力學與波動力學完全等價,它是同一種力學規律的兩種不同形式的表述。事實上,量子理論還可以更為普遍的表述出來,這是狄拉克和約爾丹的工作。
量子物理學的建立是許多物理學家共同努力的結晶,它標誌著物理學研究工作第一次集體的勝利。
實驗現象
光電效應
1905年,
阿爾伯特·愛因斯坦通過擴展普朗克的量子理論,提出不僅僅物質與電磁輻射之間的相互作用是量子化的,而且量子化是一個基本物理特性的理論。通過這個新理論,他得以解釋光電效應。
海因里希·魯道夫·赫茲和
菲利普·萊納德等人的實驗,發現通過光照,可以從金屬中打出電子來。同時他們可以測量這些電子的動能。不論入射光的強度,只有當光的頻率,超過一個臨限值(截止頻率)後,才會有電子被射出。此後被打出的電子的動能,隨光的頻率線性升高,而光的強度僅決定射出的電子的數量。愛因斯坦提出了光的量子(光子這個名稱後來才出現)的理論,來解釋這個現象。光的量子的能量為hν
在光電效應中這個能量被用來將金屬中的電子射出(逸出功
)和加速電子(動能):
愛因斯坦光電效應方程:
這裡m是電子的質量,v是其速度,v為入射光的頻率。
原子能級躍遷
20世紀初
盧瑟福模型是當時被認為正確的原子模型。這個模型假設帶負電荷的電子,像行星圍繞太陽運轉一樣,圍繞帶正電荷的原子核運轉。在這個過程中庫侖力與離心力必須平衡。這個模型有兩個問題無法解決。首先,按照
經典電磁學,這個模型不穩定。按照
電磁學,電子不斷地在它的運轉過程中被加速,同時應該通過放射電磁波喪失其能量,這樣它很快就會墜入
原子核。其次原子的發射光譜,由一系列離散的發射線組成,比如氫原子的發射光譜由一個紫外線系列(
賴曼系)、一個可見光系列(
巴耳末系)和其它的紅外線系列組成。按照經典理論原子的發射譜應該是連續的。
1913年,
尼爾斯·玻爾提出了以他命名的玻爾模型,這個模型為原子結構和光譜線,給出了一個理論原理。玻爾認為電子只能在一定能量En的軌道上運轉。假如一個電子,從一個能量比較高的軌道(En),躍到一個能量比較低的軌道(Em)上時,它發射的光的頻率為。
通過吸收同樣頻率的光子,可以從低能的軌道,躍到高能的軌道上。
玻爾模型可以解釋氫原子,改善的
玻爾模型,還可以解釋只有一個電子的離子,即He+,Li2+,Be3+等。但無法準確地解釋其它原子的
物理現象。
電子的波動性
德布羅意假設,電子也同時伴隨著一個波,他預言電子在通過一個小孔或者晶體的時候,應該會產生一個可觀測的衍射現象。1925年,當戴維孫和革末在進行電子在鎳晶體中的散射實驗時,首次得到了電子在晶體中的衍射現象。當他們了解到德布羅意的工作以後,於1927年又較精確地進行了這個實驗。實驗結果與德布羅意波的公式完全符合,從而有力地證明了電子的波動性。
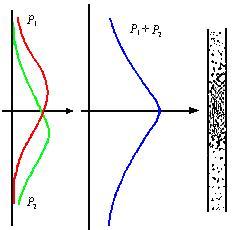
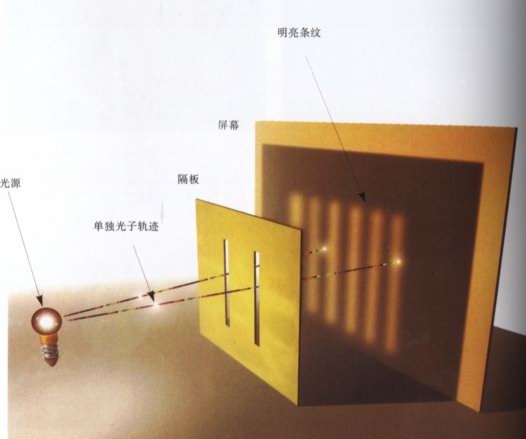
電子的波動性也同樣表現在電子在通過雙狹縫時的干涉現象中。如果每次只發射一個電子,它將以波的形式通過雙縫後,在感光屏上隨機地激發出一個小亮點。多次發射單個電子或者一次發射多個電子,感光屏上將會出現明暗相間的干涉條紋。這就再次證明了電子的波動性。
電子打在螢幕上的位置,有一定的分布
機率,隨時間可以看出雙縫衍射所特有的條紋圖像。假如一個光縫被關閉的話,所形成的圖像是單縫特有的波的分布機率。
從來不可能有半個電子,在這個電子的雙縫干涉實驗中,它是電子以波的形式同時穿過兩條縫,自己與自己發生了干涉,不能錯誤地認為是兩個不同的電子之間的干涉。值得強調的是這裡波函式的疊加是機率幅的疊加而不是如經典例子那樣的機率疊加,這個“態疊加原理”是量子力學的一個基本假設。
相關概念
波和粒子
振動粒子的量子論詮釋
物質的粒子性由能量E 和
動量p 刻劃,
波的特徵則由電磁波頻率γ 和其波長λ 表達,這兩組物理量的比例因子由
普朗克常數h(h=6.626*10^(-34)J·s) 所聯繫。
E=hγ , E=mc^2 聯立兩式,得:m=hγ/c^2(這是光子的相對論質量,由於光子無法靜止,因此光子無靜質量)而p=mv
則p=vhγ/c^{2}(p 為動量)
粒子波的一維平面波的偏微分波動方程,其一般形式為
 量子力學
量子力學dξ/dx=(1/γ)(dξ/dt) [5]
dξ/dx+dξ/dy+dξ/dz=(1/γ)(dξ/dt) [6]
波動方程是借用經典力學中的波動理論,對微觀粒子波動性的一種描述。通過這個橋樑,使得量子力學中的波粒二象性得到了很好的表達。
經典波動方程1,1'式或[6]式中的u,隱含著不連續的量子關係E=hγ和德布羅意關係λ=h/p,由於u=γλ,故可在u=vλ的右邊乘以含普朗克常數h的因子(h/h),就得到
u=(γh)(λ/h)
=E/p
 德布羅意
德布羅意等關係u=E/p,使
經典物理與
量子物理,連續與不連續(定域)之間產生了聯繫,得到統一 .
粒子波 德布羅意物質波
德布羅意關係λ=h/p,和量子關係E=hγ(及
薛丁格方程)這兩個關係式實際表示的是波動性與粒子性的統一關係, 德布羅意物質波是波粒一體的真物質粒子,光子,電子等的波動.
海森堡不確定性原理
即物體動量的不確定性乘以其位置的不確定性大於等於1/2的約化普朗克常數。
測量過程
量子力學與經典力學的一個主要區別,在於測量過程在理論中的地位。在經典力學中,一個物理系統的位置和動量,可以無限精確地被確定和被預言。至少在理論上,測量對這個系統本身,並沒有任何影響,並可以無限精確地進行。在量子力學中,測量過程本身對系統造成影響。
要描寫一個可觀察量的測量,需要將一個系統的狀態,線性分解為該可觀察量的一組本徵態的
線性組合。測量過程可以看作是在這些本徵態上的一個投影,測量結果是對應於被投影的本徵態的本徵值。假如,對這個系統的無限多個拷貝,每一個拷貝都進行一次測量的話,我們可以獲得所有可能的測量值的
機率分布,每個值的機率等於對應的本徵態的係數的絕對值平方。
由此可見,對於兩個不同的物理量A和B的測量順序,可能直接影響其測量結果。事實上,不相容可觀察量就是這樣的。
不確定性
最著名的不相容可觀察量,它是一個粒子的位置x和動量p。它們的不確定性Δx和Δp的乘積,大於或等於
普朗克常數的一半:
海森堡1927年發現的“不確定性原理”,也常稱為“不確定關係”或者“測不準關係”,說的是兩個不對易算符所表示的力學量(如坐標和動量,時間和能量等),不可能同時具有確定的測量值。其中的一個測得越準確,另一個就測得越不準確。它說明:由於測量過程對微觀粒子行為的“干擾”,致使測量順序具有不可交換性,這是微觀現象的一個基本規律。實際上,像粒子的坐標和動量這樣的物理量,並不是本來就存在而等待著我們去測量的信息,測量不是一個簡單的“反映”過程,而是一個“變革”過程,它們的測量值取決於我們的測量方式,正是測量方式的互斥性導致了測不準關係。
機率
通過將一個狀態分解為可觀察量本徵態的線性組合,可以得到狀態在每一個本徵態的
機率幅c
i。這機率幅的絕對值平方|c
i|
2就是測量到該本徵值n
i的機率,這也是該系統處於本徵態的機率。ci可以通過將投影到各本徵態上計算出來:
因此,對於一個
系綜的完全相同系統的某一可觀察量,進行同樣地測量,一般獲得的結果是不同的;除非,該系統已經處於該可觀察量的本徵態上了。通過對系綜內,每一個同一狀態的系統,進行同樣的測量,可以獲得測量值ni的
統計分布。所有試驗,都面臨著這個測量值與量子力學的統計計算的問題。
量子糾纏
往往一個由多個粒子組成的系統的狀態,無法被分離為其組成的單個粒子的狀態,在這種情況下,單個粒子的狀態被稱為是糾纏的。糾纏的粒子有驚人的特性,這些特性違背一般的直覺。比如說,對一個粒子的測量,可以導致整個系統的
波包立刻塌縮,因此也影響到另一個、遙遠的、與被測量的粒子糾纏的粒子。這個現象並不違背
狹義相對論,因為在量子力學的層面上,在測量粒子前,你不能定義它們,實際上它們仍是一個整體。不過在測量它們之後,它們就會脫離量子糾纏這狀態。
量子退相干
作為一個基本理論,量子力學原則上,應該適用於任何大小的物理系統,也就是說不僅限於微觀系統,那么,它應該提供一個過渡到巨觀“經典”物理的方法。量子現象的存在提出了一個問題,即怎樣從量子力學的觀點,解釋巨觀系統的經典現象。尤其無法直接看出的是,量子力學中的疊加狀態,如何套用到巨觀世界上來。1954年,愛因斯坦在給馬克斯·波恩的信中,就提出了怎樣從量子力學的角度,來解釋巨觀物體的定位的問題,他指出僅僅量子力學現象太“小”無法解釋這個問題。
直到1970年左右,人們才開始真正領會到,上述的思想實驗,實際上並不實際,因為它們忽略了不可避免的與周圍環境的相互作用。事實證明,疊加狀態非常容易受周圍環境的影響。比如說,在
雙縫實驗中,電子或
光子與空氣分子的碰撞或者發射輻射,就可以影響到對形成衍射非常關鍵的各個狀態之間的相位的關係。在量子力學中,這個現象被稱為量子退相干。它是由系統狀態與周圍環境影響的相互作用導致的。這個相互作用可以表達為每個系統狀態與環境狀態的糾纏。其結果是只有在考慮整個系統時(即實驗系統+
環境系統)疊加才有效,而假如孤立地只考慮實驗系統的系統狀態的話,那么就只剩下這個系統的“經典”分布了。量子退相干是今天量子力學解釋巨觀量子系統的經典性質的主要方式。
量子退相干是實現量子計算機最大的攔路虎。在一台量子計算機中,需要多個量子狀態儘可能地長時間保持疊加。退相干時間短是一個非常大的技術問題。
理論演變
理論的產生及其發展
量子力學是描述物質微觀世界結構、運動與變化規律的物理科學。它是20世紀人類文明發展的一個重大飛躍,量子力學的發現引發了一系列劃時代的科學發現與技術發明,對人類社會的進步做出重要貢獻。
19世紀末正當經典物理取得重大成就的時候,一系列經典理論無法解釋的現象一個接一個地發現了。德國物理學家維恩通過熱輻射能譜的測量發現的熱輻射定理。德國物理學家
普朗克為了解釋熱輻射能譜提出了一個大膽的假設:在熱輻射的產生與吸收過程中能量是以hf為最小單位,一份一份交換的。這個能量量子化的假設不僅強調了熱輻射能量的不連續性,而且跟"輻射能量與頻率無關,由振幅確定"的基本概念直接相矛盾,無法納入任何一個經典範疇。當時只有少數科學家認真研究這個問題。
愛因斯坦於1905年提出了光量子說。1914年,美國物理學家密立根發表了光電效應實驗結果,驗證了愛因斯坦的光量子說。
1913年
丹麥物理學家玻爾為解決盧瑟福原子行星模型的不穩定性(按經典理論,原子中電子繞原子核作圓周運動要輻射能量,導致軌道半徑縮小直到跌落進原子核),提出定態假設:原子中的電子並不像行星一樣可在任意經典力學的軌道上運轉,穩定軌道的
作用量fpdq必須為h的整數倍(角動量量子化),即fpdq=nh,n稱之為
量子數。玻爾又提出原子發光過程不是經典輻射,是電子在不同的穩定軌道態之間的不連續的躍遷過程,光的頻率由軌道態之間的能量差
確定,即頻率法則。這樣,玻爾原子理論以它簡單明晰的圖像解釋了氫原子分立光譜線,並以電子軌道態直觀地解釋了化學元素周期表,導致了72號元素鉿的發現,在隨後的短短十多年內引發了一系列的重大科學進展。這在物理學史上是空前的。
 愛因斯坦
愛因斯坦由於量子論的深刻內涵,以玻爾為代表的
哥本哈根學派對此進行了深入的研究,他們對對應原理、矩陣力學、不相容原理、測不準關係、
互補原理。量子力學的幾率解釋等都做出了貢獻。
1923年4月美國物理學家康普頓發表了X射線被電子散射所引起的頻率變小現象,即康普頓效應。按經典波動理論,靜止物體對波的散射不會改變頻率。而按愛因斯坦光量子說這是兩個“粒子”碰撞的結果。光量子在碰撞時不僅將能量傳遞而且也將動量傳遞給了電子,使光量子說得到了實驗的證明。
光不僅僅是電磁波,也是一種具有能量動量的粒子。1924年美籍奧地利物理學家泡利發表了“不相容原理”:原子中不能有兩個電子同時處於同一
量子態。這一原理解釋了原子中電子的殼層結構。這個原理對所有實體物質的基本粒子(通常稱之為費米子,如質子、中子、
夸克等)都適用,構成了
量子統計力學———費米統計的基點。為解釋光譜線的精細結構與反常塞曼效應,泡利建議對於原於中的電子軌道態,除了已有的與經典力學量(能量、角動量及其分量)對應的三個量子數之外應引進第四個量子數。這個量子數後來稱為“
自旋”,是表述
基本粒子一種內在性質的物理量。
1924年,法國物理學家德布羅意提出了表達
波粒二象性的愛因斯坦———德布羅意關係:E=hV,p=h/入,將表征粒子性的物理量能量、動量與表征波性的頻率、波長通過一個常數h相等。
1925年,德國物理學家海森伯和玻爾,建立了量子理論第一個數學描述———矩陣力學。1926年,奧地利科學家提出了描述物質波連續時空演化的
偏微分方程———薛丁格方程,給出了量子論的另一個數學描述——波動力學。1948年,
費曼創立了量子力學的路徑積分形式。
量子力學在高速、微觀的現象範圍內具有普遍適用的意義。它是現代
物理學基礎之一,在現代科學技術中的表面物理、
半導體物理、凝聚態物理、粒子物理、低溫
超導物理、量子化學以及分子生物學等學科的發展中,都有重要的理論意義。量子力學的產生和發展標誌著人類認識自然實現了從巨觀世界向
微觀世界的重大飛躍。
與經典物理學的界限
1923年,
尼爾斯·玻爾提出了
對應原理,認為量子數(尤其是
粒子數)高到一定的極限後的量子系統,可以很精確地被經典理論描述。這個原理的背景是,事實上,許多巨觀系統,可以非常精確地被經典理論,如經典力學和電磁學來描寫。因此一般認為在非常“大”的系統中,量子力學的特性,會逐漸退化到經典物理的特性,兩者並不相牴觸。因此,對應原理是建立一個有效的量子力學模型的重要輔助工具。
量子力學的數學基礎是非常廣泛的,它僅要求狀態空間是
希爾伯特空間,其可觀察量是線性的算符。但是,它並沒有規定在實際情況下,哪一種希爾伯特空間、哪些算符應該被選擇。因此,在實際情況下,必須選擇相應的希爾伯特空間和算符來描寫一個特定的量子系統。而對應原理則是做出這個選擇的一個重要輔助工具。這個原理要求量子力學所做出的預言,在越來越大的系統中,逐漸近似經典理論的預言。這個大系統的極限,被稱為“經典極限”或者“對應極限”。因此可以使用啟發法的手段,來建立一個量子力學的模型,而這個模型的極限,就是相應的經典物理學的模型。
與狹義相對論的結合
量子力學在其發展初期,沒有顧及到狹義相對論。比如說,在使用諧振子模型的時候,特別使用了一個非
相對論的
諧振子。在早期,物理學家試圖將量子力學與狹義相對論聯繫到一起,包括使用相應的
克萊因-高登方程,或者
狄拉克方程,來取代薛丁格方程。這些方程雖然在描寫許多現象時已經很成功,但它們還有缺陷,尤其是它們無法描寫相對論狀態下,粒子的產生與消滅。通過量子場論的發展,產生了真正的相對論量子理論。量子場論不但將可觀察量如能量或者動量量子化了,而且將媒介相互作用的場量子化了。第一個完整的量子場論是
量子電動力學,它可以完整地描寫電磁相互作用。
一般在描寫
電磁系統時,不需要完整的量子場論。一個比較簡單的模型,是將帶電荷的粒子,當作一個處於經典電磁場中的量子力學物體。這個手段從量子力學的一開始,就已經被使用了。比如說,氫原子的電子狀態,可以近似地使用經典的1/r電壓場來計算。但是,在電磁場中的量子起伏起一個重要作用的情況下,(比如帶電粒子發射一顆光子)這個近似方法就失效了。
強弱相互作用
萬有引力
至今為止,僅僅
萬有引力無法使用量子力學來描述。因此,在
黑洞附近,或者將整個宇宙作為整體來看的話,量子力學可能遇到了其適用邊界。使用量子力學,或者使用
廣義相對論,均無法解釋,一個粒子到達黑洞的
奇點時的物理狀況。廣義相對論預言,該粒子會被壓縮到密度無限大;而量子力學則預言,由於粒子的位置無法被確定,因此,它無法達到密度無限大,而可以逃離黑洞。因此20世紀最重要的兩個新的物理理論,量子力學和廣義相對論互相矛盾。尋求解決這個矛盾的答案,是理論物理學的一個重要目標(
量子引力)。但是至今為止,找到引力的量子理論的問題,顯然非常困難。雖然,一些亞經典的近似理論有所成就,比如對
霍金輻射的預言,但是至今為止,無法找到一個整體的量子引力的理論。這個方面的研究包括
弦理論等。
套用學科
在上述這些發明創造中,量子力學的概念和數學描述,往往很少直接起了一個作用,而是
固體物理學、化學、
材料科學或者
核物理學的概念和規則,起了主要作用,在所有這些學科中,量子力學均是其基礎,這些學科的基本理論,全部是建立在量子力學之上的。以下僅能列舉出一些最顯著的量子力學的套用,而且,這些列出的例子,肯定也非常不完全。
原子物理學
原子物理和化學
任何物質的化學特性,均是由其原子和分子的電子結構所決定的。通過解析包括了所有相關的
原子核和電子的多粒子薛丁格方程,可以計算出該原子或分子的電子結構。在實踐中,人們認識到,要計算這樣的方程實在太複雜,而且在許多情況下,只要使用簡化的模型和規則,就足以確定物質的化學特性了。在建立這樣的簡化的模型中,量子力學起了一個非常重要的作用。
一個在化學中非常常用的模型是
原子軌道。在這個模型中,分子的電子的多粒子狀態,通過將每個原子的電子單粒子狀態加到一起形成。這個模型包含著許多不同的近似(比如忽略電子之間的排斥力、電子運動與原子核運動脫離等等),它可以近似地、準確地描寫原子的
能級。除比較簡單的計算過程外,這個模型還可以直覺地給出電子排布以及軌道的圖像描述。
通過原子軌道,人們可以使用非常簡單的原則(
洪德定則)來區分電子排布。化學穩定性的規則(八隅律、幻數)也很容易從這個量子力學模型中推導出來。
通過將數個原子軌道加在一起,可以將這個模型擴展為分子軌道。由於分子一般不是球對稱的,因此這個計算要比原子軌道要複雜得多。理論化學中的分支,
量子化學和
計算機化學,專門使用近似的薛丁格方程,來計算複雜的分子的結構及其化學特性的學科。
原子核物理學
原子核物理學是研究原子核性質的物理學分支。它主要有三大領域:研究各類次原子粒子與它們之間的關係、分類與分析原子核的結構、帶動相應的核子技術進展。
固體物理學
為什麼金剛石硬、脆和透明,而同樣由碳組成的石墨卻軟而不透明?為什麼金屬導熱、導電,有金屬光澤?發光二極體、二極體和三極體的工作原理是什麼?鐵為什麼有鐵磁性?超導的原理是什麼?
以上這些例子,可以使人想像到
固體物理學的多樣性。事實上,凝聚態物理學是物理學中最大的分支,而所有
凝聚態物理學中的現象,從微觀角度上,都只有通過量子力學,才能正確地被解釋。使用經典物理,頂多只能從表面上和現象上,提出一部分的解釋。
以下列出了一些量子效應特彆強的現象:
晶格現象 | 聲子、熱傳導 |
靜電現象 | 壓電效應 |
電導 | 絕緣體、導體 |
磁性 | 鐵磁性 |
低溫態 | 玻色-愛因斯坦凝聚 |
低維效應 | 量子線、量子點 |
量子信息學
研究的焦點在於一個可靠的、處理量子狀態的方法。由於量子狀態可以疊加的特性。理論上,量子計算機可以高度平行運算。它可以套用在
密碼學中。理論上,
量子密碼術可以產生理論上絕對安全的密碼。另一個當前的研究項目,是將量子狀態利用量子糾纏態傳送到遠處的量子隱形傳送。
量子力學解釋
量子力學問題
按動力學意義上說,量子力學的運動方程是,當體系的某一時刻的狀態被知道時,可以根據運動方程預言它的未來和過去任意時刻的狀態。
量子力學的預言和
經典物理學運動方程(質點運動方程和波動方程)的預言在性質上是不同的。在經典物理學理論中,對一個體系的測量不會改變它的狀態,它只有一種變化,並按運動方程演進。因此,運動方程對決定體系狀態的力學量可以作出確定的預言。
量子力學可以算作是被驗證的最嚴密的物理理論之一了。至今為止,所有的實驗數據均無法推翻量子力學。大多數物理學家認為,它“幾乎”在所有情況下,正確地描寫能量和物質的物理性質。雖然如此,量子力學中,依然存在著概念上的弱點和缺陷,除上述的
萬有引力的量子理論的缺乏外,至今為止對量子力學的解釋存在著爭議。
解釋
假如,量子力學的數學模型,它的適用範圍內的完整的物理現象的描寫的話,我們發現測量過程中,每次測量結果的機率性的意義,與經典統計理論中的機率,意義不同。即使完全相同的系統的測量值,也會是隨機的。這與經典的統計力學中的機率結果不一樣。在經典的統計力學中,測量結果的不同,它是由於實驗者無法完全複製一個系統,而不是因為測量儀器無法精確地進行測量。在量子力學的標準解釋中,測量的隨機性是基本性的,它是由量子力學的理論基礎獲得的。由於量子力學儘管無法預言單一實驗的結果,依然是一個完整的自然的描寫,使得人們不得不得出以下結論:世界上不存在通過單一測量可以獲得的客觀的系統特性。一個量子力學狀態的客觀特性,只有在描寫其整組實驗所體現出的統計分布中,才能獲得。愛因斯坦(“量子力學不完整”,“上帝不擲骰子”)與尼爾斯·玻爾是最早對這個問題進行爭論的。玻爾維護
不確定原理和
互補原理。在多年的、激烈的討論中,
愛因斯坦不得不接受不確定原理,而玻爾則削弱了他的互補原理,這最後導致了今天的
哥本哈根詮釋。
今天,大多數物理學家,接受了量子力學描述所有一個系統可知的特性,以及測量過程無法改善,不是因為我們的技術問題所導致的的見解。這個解釋的一個結果是,測量過程擾動薛丁格方程,使得系統塌縮到它的本徵態。除哥本哈根詮釋外,還有人提出過一些其它解釋方式。包括:
1.
戴維·玻姆提出了一個不局部的,帶有隱變數的理論(
隱變數理論)。在這個解釋中,波函式被理解為粒子的一個引波。從結果上,這個理論預言的實驗結果,與非
相對論哥本哈根詮釋的預言完全一樣,因此,使用實驗手段無法鑑別這兩個解釋。雖然,這個理論的預言是決定性的,但是,由於不確定原理無法推測出隱變數的精確狀態。其結果是與哥本哈根詮釋一樣,使用這來解釋實驗的結果,也是一個機率性的結果。至今為止,還不能確定這個解釋,是否能夠擴展到
相對論量子力學上去。路易斯·德布羅意和其他人也提出過類似的隱藏係數解釋。
2.
休·艾弗雷特三世提出的多世界詮釋認為,所有
量子理論所做出的可能性的預言,全部同時實現,這些現實成為互相之間一般無關的平行宇宙。在這個詮釋中,總的
波函式不塌縮,它的發展是決定性的。但是由於我們作為觀察者,無法同時在所有的平行宇宙中存在,因此,我們只觀察到在我們的宇宙中的測量值,而在其它宇宙中的平行,我們則觀察到他們的宇宙中的測量值。這個詮釋不需要對測量的特殊的對待。
薛丁格方程在這個理論中所描寫的也是所有平行宇宙的總和。
3.
微觀作用原理認為(詳見《
量子筆跡》),微觀粒子之間存在微觀作用力(微觀作用力既可以演化到巨觀力學也可以演化到微觀力學),微觀作用是量子力學背後更深層次的理論,微觀粒子之所以表現出波動性是對微觀作用力的間接客觀反映,在微觀作用原理之下量子力學面臨的難題和困惑得到理解和解釋。
4.另一個解釋方向是將經典邏輯改成一個量子邏輯來排除解釋的困難。
以下列舉了對量子力學的解釋,最重要的實驗和思想實驗:
1.愛因斯坦-波多斯基-羅森悖論以及相關的
貝爾不等式,明顯地顯示了,量子力學理論無法使用“局部”隱變數來解釋;不排除非局部隱藏係數的可能性。
2.
雙縫實驗是一個非常重要的量子力學試驗,從這個試驗中,也可以看到量子力學的測量問題和解釋的困難性,這是最簡單而明顯地顯示
波粒二象性的試驗了。
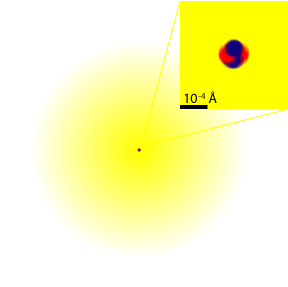 電子云
電子云 普朗克
普朗克




 波粒二象性
波粒二象性
 薛丁格
薛丁格 海森堡
海森堡 狄拉克
狄拉克 玻爾
玻爾




 量子力學
量子力學 電子云
電子云
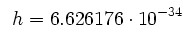 值
值 光電效應
光電效應



 量子力學
量子力學 德布羅意
德布羅意
 愛因斯坦
愛因斯坦