基本介紹
- 中文名:狄拉克方程
- 外文名:Dirac Equation
- 提出方程:電子運動的相對論性量子力學方程
- 提出者:狄拉克
- 時間:1928年
- 分類:物理 數學
概念
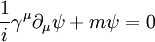 自然單位制下的狄拉克方程
自然單位制下的狄拉克方程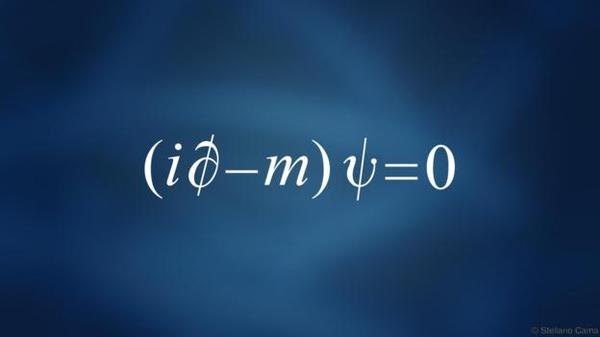
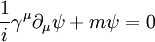 自然單位制下的狄拉克方程
自然單位制下的狄拉克方程1928年英國物理學家狄拉克提出的方程。利用這個方程研究氫原子能級分布時,考慮有自旋角動量的電子作高速運動時的相對論性效應,給出了氫原子能級的精細結構,與實驗...
理論物理中,相對於薛丁格方程之於非相對論量子力學,狄拉克方程是相對論量子力學的一項描述自旋-½粒子的波函式方程,由英國物理學家保羅·狄拉克於1928年建立,不帶...
狄拉克理論就是指狄拉克在純數學物理的基礎上建立起了狄拉克方程,並預言存在一種新的基本粒子——正電子。幾年後,在實驗室里發現了這種粒子。在1926年薛丁格發表...
狄拉克預言指的是,1931年著名的英國物理學家狄拉克首先從理論上用極精美的數學物理公式預言,磁單極子是可以獨立存在的。他認為,既然電有基本電荷電子存在,磁也應...
保羅·狄拉克,OM,FRS(Paul Adrien Maurice Dirac,1902年8月8日-1984年10月20日),男,英國理論物理學家,量子力學的奠基者之一,並對量子電動力學早期的發展作出...
馬約拉納方程是相對論性的波動方程。它與狄拉克方程相似,然而式子中包含了粒子的共軛。此方程由義大利物理學家埃托雷·馬約拉納(Ettore Majorana)提出。...
這兩個問題使得克萊因-戈爾登方程在很長一段時間裡被認為是缺乏物理意義的.英國物理學家保羅·狄拉克為了確保機率密度具有物理意義建立了狄拉克方程,但這個方程仍然...
量子場論中,狄拉克旋量(英語:Dirac spinor)為一雙旋量,出現在自由粒子狄拉克方程的平面波解中。...
狄拉克空穴理論,是狄拉克根據泡利不相容原理提出的。所謂空穴,就是我們現在所知道的正電子。他認為所謂真空狀態並非真的空無一物,而是所有負能態都被電子占有,形成...
1928年英國物理學家狄拉克(Paul Adrien MauriceDirac)提出了一個電子運動的相對論性量子力學方程,即狄拉克方程。利用這個方程研究氫原子能級分布時,考慮有自旋角動量...
電子的相對論量子力學方程——狄拉克方程可解出自由電子的負能級,按能量最低原理,物質世界的電子都應躍遷到負能級上,迪拉克對此做出的解釋是這些負能級已被電子占據...
阿布拉罕-勞侖茲-狄拉克力(Abraham-Lorentz-Dirac force)是阿布拉罕-勞侖茲力的改版,跟阿布拉罕-勞侖茲力一樣,是描述當加速帶電粒子因為粒子放射出電磁輻射而所受到...
狄拉克對物理學的主要貢獻是發展了量子力學,提出了著名的狄拉克方程,並且從理論上預言了正電子的存在。狄拉克青年時代正好是原子物理學實驗積累了大量材料、量子理論...
由ψ所描寫的自旋為1/2的場就稱為旋量場。旋量場是由狄拉克方程中引入的,與狄拉克方程有關。量子場論中,場量ψ是一個算符,它表示粒子的湮沒和反粒子的...
(15),括弧中的兩位數字為測量的不確定度,來源於標準差,整數部分2來源於狄拉克方程(狄拉克方程是與將電子自旋與其電磁性質聯繫起來的基本方程),小數部分(0.002...
他長期從事科學研究,創立量子電動力學;1928年建立“狄拉克方程”,即相對論形式的薛丁格方程;這個貌似簡單的方程式從理論上預言了正電子的存在,具有劃時代的意義;它...
