基本介紹
- 中文名:不確定性原理
- 外文名:Uncertainty principle
- 別稱:測不準原理;不確定原理
- 表達式:ΔxΔp≥h/4π
- 提出者:維爾納·海森堡(Werner Heisenberg)
- 提出時間:1927年
- 套用學科:物理
- 適用領域範圍:量子力學
定律定義,不確定性原理,簡介,定律影響,發展簡史,舊量子論,質疑,現代不等式,名稱,理論背景,海森堡,與玻爾的辯論,玻爾理論,霍金觀點,決定論,宿命論,量子假設,量子假設意義,影響,量子力學,
定律定義
不確定性原理
德國物理學家海森堡1927年提出的不確定性原理是量子力學的產物。這項原則陳述了精確確定一個粒子,例如原子周圍的電子的位置和動量是有限制。這個不確定性來自兩個因素,首先測量某東西的行為將會不可避免地擾亂那個事物,從而改變它的狀態;其次,因為量子世界不是具體的,但基於機率,精確確定一個粒子狀態存在更深刻更根本的限制。
海森堡測不準原理是通過一些實驗來論證的。構想用一個γ射線顯微鏡來觀察一個電子的坐標,因為γ射線顯微鏡的分辨本領受到波長λ的限制,所用光的波長λ越短,顯微鏡的解析度越高,從而測定電子坐標不確定的程度 就越小,所以
就越小,所以 。但另一方面,光照射到電子,可以看成是光量子和電子的碰撞,波長λ越短,光量子的動量就越大,所以有
。但另一方面,光照射到電子,可以看成是光量子和電子的碰撞,波長λ越短,光量子的動量就越大,所以有 。
。



再比如,用將光照到一個粒子上的方式來測量一個粒子的位置和速度,一部分光波被此粒子散射開來,由此指明其位置。但人們不可能將粒子的位置確定到比光的兩個波峰之間的距離更小的程度,所以為了精確測定粒子的位置,必須用短波長的光。
但普朗克的量子假設,人們不能用任意小量的光:人們至少要用一個光量子。這量子會擾動粒子,並以一種不能預見的方式改變粒子的速度。
所以,簡單來說,就是如果要想測定一個量子的精確位置的話,那么就需要用波長儘量短的波,這樣的話,對這個量子的擾動也會越大,對它的速度測量也會越不精確;如果想要精確測量一個量子的速度,那就要用波長較長的波,那就不能精確測定它的位置。
於是,經過一番推理計算,海森堡得出:△q△p≥ħ/2(ħ=h/2π)。海森堡寫道:“在位置被測定的一瞬,即當光子正被電子偏轉時,電子的動量發生一個不連續的變化,因此,在確知電子位置的瞬間,關於它的動量我們就只能知道相應於其不連續變化的大小的程度。於是,位置測定得越準確,動量的測定就越不準確,反之亦然。”
海森堡還通過對確定原子磁矩的斯特恩-蓋拉赫實驗的分析證明,原子穿過偏轉所費的時間△T越長,能量測量中的不確定性△E就越小。再加上德布羅意關係λ=h/p,海森伯得到△E△T≥h/4π,並且作出結論:“能量的準確測定如何,只有靠相應的對時間的測不準量才能得到。”
簡介
其中,h 是普朗克常數。
長久以來,不確定性原理與另一種類似的物理效應(稱為觀察者效應)時常會被混淆在一起。觀察者效應指出,對於系統的測量不可避免地會影響到這系統。為了解釋量子不確定性,海森堡的表述所援用的是量子層級的觀察者效應。之後,物理學者漸漸發覺,肯納德的表述所涉及的不確定性原理是所有類波系統的內秉性質,它之所以會出現於量子力學完全是因為量子物體的波粒二象性,它實際表現出量子系統的基礎性質,而不是對於當今科技實驗觀測能力的定量評估。在這裡特彆強調,測量不是只有實驗觀察者參與的過程,而是經典物體與量子物體之間的相互作用,不論是否有任何觀察者參與這過程。
類似的不確定性關係式也存在於能量和時間、角動量和角度等物理量之間。由於不確定性原理是量子力學的重要結果,很多一般實驗都時常會涉及到關於它的一些問題。有些實驗會特別檢驗這原理或類似的原理。例如,檢驗發生於超導系統或量子光學系統的“數字-相位不確定性原理”。對於不確定性原理的相關研究可以用來發展引力波干涉儀所需要的低噪聲科技。
定律影響
該原理表明:一個微觀粒子的某些物理量(如位置和動量,或方位角與動量矩,還有時間和能量等),不可能同時具有確定的數值,其中一個量越確定,另一個量的不確定程度就越大。測量一對共軛量的誤差(標準差)的乘積必然大於常數h/4π(h是普朗克常數)是海森堡在1927年首先提出的,它反映了微觀粒子運動的基本規律——以共軛量為自變數的機率幅函式(波函式)構成傅立葉變換對;以及量子力學的基本關係( ),是物理學中又一條重要原理。
),是物理學中又一條重要原理。

發展簡史
舊量子論
緊跟在漢斯·克拉默斯(Hans Kramers)的開拓工作之後,1925年6月,維爾納·海森堡發表論文《運動與機械關係的量子理論重新詮釋》(Quantum-Theoretical Re-interpretation of Kinematic and Mechanical Relations),創立了矩陣力學。舊量子論漸漸式微,現代量子力學正式開啟。矩陣力學大膽地假設,關於運動的經典概念不適用於量子層級。在原子裡的電子並不是運動於明確的軌道,而是模糊不清,無法觀察到的軌域;其對於時間的傅立葉變換隻涉及從量子躍遷中觀察到的離散頻率。
海森堡在論文裡提出,只有在實驗裡能夠觀察到的物理量才具有物理意義,才可以用理論描述其物理行為,其它都是無稽之談。因此,他避開任何涉及粒子運動軌道的詳細計算,例如,粒子隨著時間而改變的確切運動位置。因為,這運動軌道是無法直接觀察到的。替代地,他專注於研究電子躍遷時,所發射的光的離散頻率和強度。他計算出代表位置與動量的無限矩陣。這些矩陣能夠正確地預測電子躍遷所發射出光波的強度。
同年6月,海森堡的上司馬克斯·玻恩,在閱讀了海森堡交給他發表的論文後,發覺了位置與動量無限矩陣有一個很顯著的關係──它們不互相對易。這關係稱為正則對易關係,以方程表示為:

在那時,物理學者還沒能清楚地了解這重要的結果,他們無法給予合理的詮釋。
質疑
小澤不等式及其驗證
日本名古屋大學教授小澤正直和奧地利維也納工科大學副教授長谷川祐司的科研團隊通過實驗發現,大約在80年前提出的用來解釋微觀世界中量子力學的基本定律“測不準原理”有其缺陷所在。該發現在全世界尚屬首次。這個發現成果被稱作是應面向高速密碼通信技術套用和教科書改換的形勢所迫,於2012年1月15日在英國科學雜誌《自然物理學》(電子版)上發表。
弱測量技術
多倫多大學(the University of Toronto)量子光學研究小組的李·羅澤馬(Lee Rozema)設計了一種測量物理性質的儀器,其研究成果發表在2012年9月7日當周的《物理評論通訊》(Physical Review Letters)周刊上。
為了達到這個目標,需要在光子進入儀器前進行測量,但是這個過程也會造成干擾。為了解決這個問題,羅澤馬及其同事使用一種弱測量技術(weak measurement),讓所測對象受到的干擾微乎其微,每個光子進入儀器前,研究人員對其弱測量,然後再用儀器測量,之後對比兩個結果。發現造成的干擾不像海森貝格原理中推斷的那么大。
這一發現是對海森貝格理論的挑戰。2010年,澳大利亞格里菲斯大學(Griffith University)科學家倫德(A.P. Lund)和懷斯曼(Howard Wiseman)發現弱測量可以套用於測量量子體系,然而還需要一個微型量子計算機,但這種計算機很難生產出來。羅澤馬的實驗包括套用弱測量和通過“簇態量子計算”技術簡化量子計算過程,把這兩者結合,找到了在實驗室測試倫德和懷斯曼觀點的方法。
現代不等式
海森堡與玻爾共同討論問題
1926年,海森堡任聘為哥本哈根大學尼爾斯·玻爾研究所的講師,幫尼爾斯·玻爾做研究。在那裡,海森堡表述出不確定性原理,從而為後來知名為哥本哈根詮釋奠定了的堅固的基礎。海森堡證明,對易關係可以推導出不確定性,或者,使用玻爾的術語,互補性:不能同時觀測任意兩個不對易的變數;更準確地知道其中一個變數,則必定更不準確地知道另外一個變數。
在他著名的1927年論文裡, 海森堡寫出以下公式

這公式給出了任何位置測量所造成的最小無法避免的動量不確定值。雖然他提到,這公式可以從對易關係導引出來,他並沒有寫出相關數學理論,也沒有給予和確切的定義。他只給出了幾個案例(高斯波包)的合理估算。 在海森堡的芝加哥講義里,他又進一步改善了這關係式:

1927年厄爾·肯納德(Earl Kennard)首先證明了現代不等式:

其中, 是位置標準差,
是位置標準差, 是動量標準差,
是動量標準差,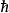 是約化普朗克常數。
是約化普朗克常數。


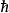
1929年,霍華德·羅伯森(Howard Robertson)給出怎樣從對易關係求出不確定關係式。
名稱
有很久一段時間,不確定性原理被稱為“測不準原理”,但實際而言,對於類波系統內秉的性質,不確定性原理與測量準確不準確並沒有直接關係(請查閱本條目稍前關於觀察者效應的內容),因此,該譯名並未正確表達出這原理的內涵。另外,英語稱此原理為“Uncertainty Principle”,直譯為“不確定性原理”,並沒有“測不準原理”這種說法,其他語言與英語的情況類似,除中文外,並無“測不準原理”一詞。現今,在中國大陸的教科書中,該原理的正式譯名也已改為“不確定性關係”(Uncertainty Relation)。
理論背景
海森堡
海森堡在創立矩陣力學時,對形象化的圖象採取否定態度。但他在表述中仍然需要使用“坐標”、“速度”之類的辭彙,當然這些辭彙已經不再等同於經典理論中的那些辭彙。可是,究竟應該怎樣理解這些辭彙新的物理意義呢?海森堡抓住雲室實驗中觀察電子徑跡的問題進行思考。他試圖用矩陣力學為電子徑跡作出數學表述,可是沒有成功。這使海森堡陷入困境。他反覆考慮,意識到關鍵在於電子軌道的提法本身有問題。人們看到的徑跡並不是電子的真正軌道,而是水滴串形成的霧跡,水滴遠比電子大,所以人們也許只能觀察到一系列電子的不確定的位置,而不是電子的準確軌道。因此,在量子力學中,一個電子只能以一定的不確定性處於某一位置,同時也只能以一定的不確定性具有某一速度。可以把這些不確定性限制在最小的範圍內,但不能等於零。這就是海森堡對不確定性最初的思考。據海森伯晚年回憶,愛因斯坦1926年的一次談話啟發了他。愛因斯坦和海森堡討論可不可以考慮電子軌道時,曾質問過海森堡:“難道說你是認真相信只有可觀察量才應當進入物理理論嗎?”對此海森堡答覆說:“你處理相對論不正是這樣的嗎?你曾強調過絕對時間是不許可的,僅僅是因為絕對時間是不能被觀察的。”愛因斯坦承認這一點,但是又說:“一個人把實際觀察到的東西記在心裡,會有啟發性幫助的……在原則上試圖單靠可觀察量來建立理論,那是完全錯誤的。實際上恰恰相反,是理論決定我們能夠觀察到的東西……只有理論,即只有關於自然規律的知識,才能使我們從感覺印象推論出基本現象。” 海森堡
海森堡
 海森堡
海森堡海森堡在1927年的論文一開頭就說:“如果誰想要闡明‘一個物體的位置’(例如一個電子的位置)這個短語的意義,那么他就要描述一個能夠測量‘電子位置’的實驗,否則這個短語就根本沒有意義。”海森堡在談到諸如位置與動量,或能量與時間這樣一些正則共軛量的不確定關係時,說:“這種不確定性正是量子力學中出現統計關係的根本原因。”
與玻爾的辯論
海森堡的測不準原理得到了玻爾的支持,但玻爾不同意他的推理方式,認為他建立測不準關係所用的基本概念有問題。雙方發生過激烈的爭論。玻爾的觀點是測不準關係的基礎在於波粒二象性,他說:“這才是問題的核心。”而海森堡說:“我們已經有了一個貫徹一致的數學推理方式,它把觀察到的一切告訴了人們。在自然界中沒有什麼東西是這個數學推理方式不能描述的。”玻爾則說:“完備的物理解釋應當絕對地高於數學形式體系。”
玻爾理論
玻爾更著重於從哲學上考慮問題。1927年玻爾作了《量子公設和原子理論的新進展》的演講,提出著名的互補原理。他指出,在物理理論中,平常大家總是認為可以不必干涉所研究的對象,就可以觀測該對象,但從量子理論看來卻不可能,因為對原子體系的任何觀測,都將涉及所觀測的對象在觀測過程中已經有所改變,因此不可能有單一的定義,平常所謂的因果性不復存在。對經典理論來說是互相排斥的不同性質,在量子理論中卻成了互相補充的一些側面。波粒二象性正是互補性的一個重要表現。測不準原理和其它量子力學結論也可從這裡得到解釋。
霍金觀點
決定論
科學理論,特別是牛頓引力論的成功,使得法國科學家拉普拉斯侯爵在19世紀初論斷,宇宙是完全被決定的。他認為存在一組科學定律,只要我們完全知道宇宙在某一時刻的狀態,我們便能依此預言宇宙中將會發生的任一事件。例如,假定我們知道某一個時刻的太陽和行星的位置和速度,則可用牛頓定律計算出在任何其他時刻的太陽系的狀態。這種情形下的宿命論是顯而易見的,拉普拉斯進一步假定存在著某些定律,它們類似地制約其他每一件東西,包括人類的行為。<續編:不確定原理實質是對因果論的一種更加肯定,可想而知,任何一種在微小的觀測都可以使對象的狀態發生改變,從而使原對象的體系進入一個新的狀態量,而在未對其干擾前他的狀態量卻會沿著一個自身作用的方向發展,(當然它的方向對我們來說是不確定的,這個不確定實質是對於我們的觀測而言的。),干擾(觀測)卻使他開始了一個“新的紀元”,而這個干擾結果對於對象而言卻是確定的,它會使對象開始一個新狀態,當然,這個新的結果又會作用於其他體系,從而影響整個宇宙。簡言之可以這么說:由於你的一個噴嚏,使氣流發生強運動,通過氣流之間力的作用,最終使美國的一朵雲達到了降水的條件,由於你的一個噴嚏,使美國降了一場雨!而沒有你的噴嚏,那個雲的運動也是一定的,降水就不可能了。所謂蝴蝶效應,其實也是這個道理,蝴蝶在太平洋那邊扇了下翅膀,另一邊可能因此颳起颱風。
妄想通過物理定律推算未來事件的努力是可笑的,從計算機學來看,這種推算是一種無限遞歸,終止遞歸的條件是得到未來某一時刻的狀態,但算法需要知道自己得出結果後計算者對環境的影響(必須考慮)因而陷入遞歸,因為終止條件是無法達成的,故算法無法完成。從可行性來看,我們生活的世界好比一台400mips的電腦環境,它是不可能模擬出一台500mips的虛擬機的。故未來不可知。
宿命論
很多人強烈地抵制這種科學決定論,他們感到這侵犯了“上帝”或神秘力量干涉世界的自由,直到20世紀初,這種觀念仍被認為是科學的標準假定。這種信念必須被拋棄的一個最初的徵兆,它是由英國科學家瑞利勳爵和詹姆斯·金斯爵士所做的計算,他們指出一個熱的物體——例如恆星——必須以無限大的速率輻射出能量。按照當時我們所相信的定律,一個熱體必須在所有的頻段同等地發出電磁波(諸如無線電波、可見光或X射線)。例如,一個熱體在1萬億赫茲到2萬億赫茲頻率之間發出和在2萬億赫茲到3萬億赫茲頻率之間同樣能量的波。而既然波的頻譜是無限的,這意味著輻射出的總能量必須是無限的。
量子假設
為了避免這顯然荒謬的結果,德國科學家馬克斯·普郎克在1900年提出,光波、X射線和其他波不能以任意的速率輻射,而必須以某種稱為量子的形式發射。並且,每個量子具有確定的能量,波的頻率越高,其能量越大。這樣,在足夠高的頻率下,輻射單獨量子所需要的能量比所能得到的還要多。因此,在高頻下輻射被減少了,物體喪失能量的速率變成有限的了。
量子假設意義
量子假設可以非常好地解釋所觀測到的熱體的發射率,直到1926年另一個德國科學家威納·海森堡提出著名的不確定性原理之後,它對宿命論的含義才被意識到。為了預言一個粒子未來的位置和速度,人們必須能準確地測量它現時的位置和速度。顯而易見的辦法是將光照到這粒子上,一部分光波被此粒子散射開來,由此指明它的位置。然而,人們不可能將粒子的位置確定到比光的兩個波峰之間距離更小的程度,所以必須用短波長的光來測量粒子的位置。由普朗克的量子假設,人們不能用任意少的光的數量,至少要用一個光量子。這量子會擾動這粒子,並以一種不能預見的方式改變粒子的速度。而且,位置測量得越準確,所需的波長就越短,單獨量子的能量就越大,這樣粒子的速度就被擾動得越厲害。換言之,你對粒子的位置測量得越準確,你對速度的測量就越不準確,反之亦然。海森堡指出,粒子位置的不確定性乘上粒子質量再乘以速度的不確定性不能小於一個確定量——普朗克常數。並且,這個極限既不依賴於測量粒子位置和速度的方法,也不依賴於粒子的種類。海森堡不確定性原理是世界的一個基本的不可迴避的性質。
影響
不確定性原理對我們世界觀有非常深遠的影響。甚至到了50多年之後,它還不為許多哲學家所鑑賞,仍然是許多爭議的主題。不確定性原理使拉普拉斯科學理論,即一個完全確定性的宇宙模型的夢想壽終正寢:如果人們甚至不能準確地測量宇宙當前的狀態,那么就肯定不能準確地預言將來的事件(否認觀察者可以確定未來)!但客觀來說宇宙當前的狀態是確定的無疑(承認客觀未來的確定性)。我們仍然可以想像,對於一些超自然的生物,存在一組完全地決定事件的定律,這些生物能夠不干擾宇宙地觀測它的狀態。然而,對於我們這些芸芸眾生而言,這樣的宇宙模型並沒有太多的興趣,因為對於我們這些觀察者來說未來的確是不可預知的。看來,最好是採用稱為奧鏗剃刀的經濟學原理,將理論中不能被觀測到的所有特徵都割除掉。20世紀20年代。在不確定性原理的基礎上,海森堡、厄文·薛丁格和保爾·狄拉克運用這種手段將力學重新表達成稱為量子力學的新理論。在此理論中,粒子不再有分別被很好定義的、能被同時觀測的位置和速度,而代之以位置和速度的結合物的量子態。
量子力學
一般而言,量子力學並不對一次觀測預言一個單獨的確定結果。代之,它預言一組不同的可能發生的結果,並告訴我們每個結果出現的機率。也就是說,如果我們對大量的類似的系統作同樣的測量,每一個系統以同樣的方式起始,我們將會找到測量的結果為A出現一定的次數,為B出現另一不同的次數等等。人們可以預言結果為A或B的出現的次數的近似值,但不能對個別測量的特定結果作出預言。因而量子力學為科學引進了不可避免的非預見性或偶然性。儘管愛因斯坦在發展這些觀念時起了很大作用,但他非常強烈地反對這些。他之所以得到諾貝爾獎就是因為對量子理論的貢獻。即使這樣,他也從不接受宇宙受機遇控制的觀點;他的感覺可表達成他著名的斷言:“上帝不玩弄骰子。”然而,大多數其他科學家願意接受量子力學,因為它和實驗符合得很完美。它的的確確成為一個極其成功的理論,並成為幾乎所有現代科學技術的基礎。它制約著電晶體和積體電路的行為,而這些正是電子設備諸如電視、計算機的基本元件。它並且是現代化學和生物學的基礎。物理科學未讓量子力學進入的唯一領域是引力和宇宙的大尺度結構。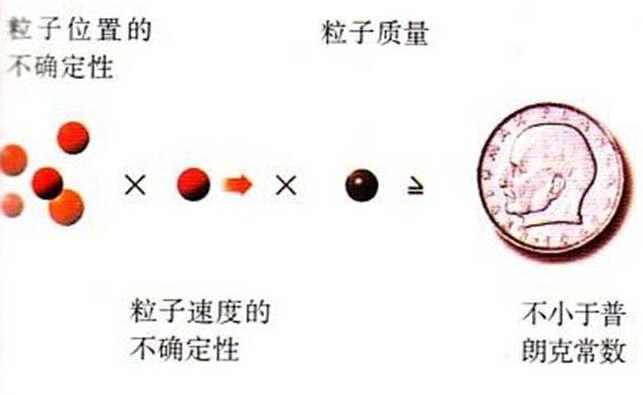 量子力學中的不確定性原理
量子力學中的不確定性原理
 量子力學中的不確定性原理
量子力學中的不確定性原理

