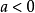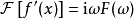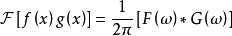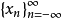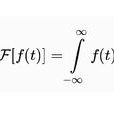傅立葉變換，表示能將滿足一定條件的某個函式表示成三角函式（正弦和/或餘弦函式）或者它們的積分的線性組合。在不同的研究領域，傅立葉變換具有多種不同的變體形式，如連續傅立葉變換和離散傅立葉變換。最初傅立葉分析是作為熱過程的解析分析的工具被提出的。
基本介紹
- 中文名：傅立葉變換
- 外文名：Fourier Transform
- 別稱：傅立葉展開
- 提出者：傅立葉
- 提出時間：1807年
- 套用學科：數位訊號處理
- 適用領域範圍：電工學，信號處理
簡介,定義,相關,性質,線性性質,尺度變換性質,對偶性,平移性質,微分關係,時域卷積定理,頻域卷積定理,Parseval定理以及Plancherel定理,特殊變換,連續傅立葉變換,傅立葉級數,離散時間傅立葉變換,相關,變換提出,為什麼用三角函式展開,時域頻域,變換分類,變換意義,傅立葉變換的推廣,例子,套用,整體結構,蝶形運算器,FFT的地址,旋轉因子,存儲器控制,
簡介
Fourier transform或Transformée de Fourier有多箇中文譯名，常見的有“傅立葉變換”、“付立葉變換”、“傅立葉轉換”、“傅氏轉換”、“傅氏變換”、等等。
定義
f(t)是t的周期函式，如果t滿足狄里赫萊條件：在一個以2T為周期內f(X)連續或只有有限個第一類間斷點，附f（x）單調或可劃分成有限個單調區間，則F（x）以2T為周期的傅立葉級數收斂，和函式S（x）也是以2T為周期的周期函式，且在這些間斷點上，函式是有限值；在一個周期內具有有限個極值點；絕對可積。則有下圖①式成立。稱為積分運算f(t)的傅立葉變換，
②式的積分運算叫做F(ω)的傅立葉逆變換。F(ω)叫做f(t)的像函式，f(t)叫做
F(ω)的像原函式。F(ω)是f(t)的像。f(t)是F(ω)原像。
①傅立葉變換
②傅立葉逆變換
傅立葉變換在物理學、電子類學科、數論、組合數學、信號處理、機率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的套用（例如在信號處理中，傅立葉變換的典型用途是將信號分解成頻率譜——顯示與頻率對應的幅值大小）。
相關
* 傅立葉變換屬於諧波分析。
* 傅立葉變換的逆變換容易求出，而且形式與正變換非常類似;
* 正弦基函式是微分運算的本徵函式，從而使得線性微分方程的求解可以轉化為常係數的代數方程的求解.線上性時不變的物理系統內，頻率是個不變的性質，從而系統對於複雜激勵的回響可以通過組合其對不同頻率正弦信號的回響來獲取；
*卷積定理指出：傅立葉變換可以化複雜的卷積運算為簡單的乘積運算，從而提供了計算卷積的一種簡單手段；
* 離散形式的傅立葉變換可以利用數字計算機快速地算出（其算法稱為快速傅立葉變換算法（FFT)).
性質
線性性質
傅立葉變換的線性，是指兩函式的線性組合的傅立葉變換，等於這兩個函式分別做傅立葉變換後再進行線性組合的結果。具體而言，假設函式
和
的傅立葉變換
和
都存在，
和
為任意常係數，則有
尺度變換性質
若函式
的傅立葉變換為
，則對任意的非零實數
，函式
的傅立葉變換
存在，且等於
對偶性
若函式 的傅立葉變換為 ，則存在
平移性質
微分關係
若函式
的傅立葉變換為
，且其導函式
的傅立葉變換存在，則有
時域卷積定理
若函式
以及
都在
上絕對可積，則卷積函式
頻域卷積定理
若
的傅立葉變換為
，
的傅立葉變換為
，則有
Parseval定理以及Plancherel定理
若函式
以及
平方可積，二者的傅立葉變換分別為
與
，則有
特殊變換
連續傅立葉變換
一般情況下，若“傅立葉變換”一詞的前面未加任何限定語，則指的是“連續傅立葉變換”。“連續傅立葉變換”將平方可積的函式
表示成復指數函式的積分形式：
上式其實表示的是連續傅立葉變換的逆變換，即將時間域的函式表示為頻率域的函式
的積分。反過來，其正變換恰好是將頻率域的函式 表示為時間域的函式
的積分形式。一般可稱函式 為原函式，而稱函式 為傅立葉變換的像函式，原函式和像函式構成一個傅立葉變換對（transform pair）。
當 為奇函式（或偶函式）時，其餘弦（或正弦）分量為零，而可以稱這時的變換為餘弦變換（或正弦變換）。
傅立葉級數
主條目：傅立葉級數
對於實值函式，函式的傅立葉級數可以寫成：
離散時間傅立葉變換
主條目：離散時間傅立葉變換
離散時間傅立葉變換（discrete-time Fourier transform, DTFT）針對的是定義域為Z的數列。設
為某一數列，則其DTFT被定義為
DTFT在時域上離散，在頻域上則是周期的，它一般用來對離散時間信號進行頻譜分析。DTFT可以被看作是傅立葉級數的逆。
離散傅立葉變換
為了在科學計算和數位訊號處理等領域使用計算機進行傅立葉變換，必須將函式定義在離散點上而非連續域內，且須滿足有限性或周期性條件。這種情況下，序列
的離散傅立葉變換（discrete Fourier transform, DFT）為
在阿貝爾群上的統一描述
以上各種傅立葉變換可以被更統一的表述成任意局部緊緻的阿貝爾群上的傅立葉變換。這一問題屬於調和分析的範疇。在調和分析中，一個變換從一個群變換到它的對偶群（dual group）。此外，將傅立葉變換與卷積相聯繫的卷積定理在調和分析中也有類似的結論。
傅立葉變換家族
下表列出了傅立葉變換家族的成員。容易發現，函式在時（頻）域的離散對應於其像函式在頻（時）域的周期性，反之連續則意味著在對應域的信號的非周期性。
相關
變換提出
傅立葉是一位法國數學家和物理學家的名字，英語原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier對熱傳遞很感興趣，於1807年在法國科學學會上發表了一篇論文，運用正弦曲線來描述溫度分布，論文裡有個在當時具有爭議性的決斷：任何連續周期信號可以由一組適當的正弦曲線組合而成。當時審查這個論文的人，其中有兩位是歷史上著名的數學家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827)，當拉普拉斯和其它審查者投票通過並要發表這個論文時，拉格朗日堅決反對，在他此後生命的六年中，拉格朗日堅持認為傅立葉的方法無法表示帶有稜角的信號，如在方波中出現非連續變化斜率。法國科學學會屈服於拉格朗日的威望，拒絕了傅立葉的工作，幸運的是，傅立葉還有其它事情可忙，他參加了政治運動，隨拿破崙遠征埃及，法國大革命後因會被推上斷頭台而一直在逃避。直到拉格朗日死後15年這個論文才被發表出來。
拉格朗日是對的：正弦曲線無法組合成一個帶有稜角的信號。但是，我們可以用正弦曲線來非常逼近地表示它，逼近到兩種表示方法不存在能量差別，基於此，傅立葉是對的。
用正弦曲線來代替原來的曲線而不用方波或三角波來表示的原因在於，分解信號的方法是無窮的，但分解信號的目的是為了更加簡單地處理原來的信號。用正餘弦來表示原信號會更加簡單，因為正餘弦擁有原信號所不具有的性質：正弦曲線保真度。一個正弦曲線信號輸入後，輸出的仍是正弦曲線，只有幅度和相位可能發生變化，但是頻率和波的形狀仍是一樣的。且只有正弦曲線才擁有這樣的性質，正因如此我們才不用方波或三角波來表示。
為什麼用三角函式展開
為什麼偏偏選擇三角函式而不用其他函式進行分解？我們從物理系統的特徵信號角度來解釋。我們知道：大自然中很多現象可以抽象成一個線性時不變系統來研究，無論你用微分方程還是傳遞函式或者狀態空間描述。線性時不變系統可以這樣理解：輸入輸出信號滿足線性關係，而且系統參數不隨時間變換。對於大自然界的很多系統，一個正弦曲線信號輸入後，輸出的仍是正弦曲線，只有幅度和相位可能發生變化，但是頻率和波的形狀仍是一樣的。也就是說正弦信號是系統的特徵向量！當然，指數信號也是系統的特徵向量，表示能量的衰減或積聚。自然界的衰減或者擴散現象大多是指數形式的，或者既有波動又有指數衰減（復指數
形式），因此具有特徵的基函式就由三角函式變成復指數函式。但是，如果輸入是方波、三角波或者其他什麼波形，那輸出就不一定是什麼樣子了。所以，除了指數信號和正弦信號以外的其他波形都不是線性系統的特徵信號。
用正弦曲線來代替原來的曲線而不用方波或三角波或者其他什麼函式來表示的原因在於：正弦信號恰好是很多線性時不變系統的特徵向量。於是就有了傅立葉變換。對於更一般的線性時不變系統，復指數信號(表示耗散或衰減)是系統的“特徵向量”。於是就有了拉普拉斯變換。z變換也是同樣的道理，這時是離散系統的“特徵向量”。這裡沒有區分特徵函式和特徵向量的概念，主要想表達二者的思想是相同的，只不過一個是有限維向量，一個是無限維函式。
傅立葉級數和傅立葉變換其實就是我們之前討論的特徵值與特徵向量的問題。分解信號的方法是無窮的，但分解信號的目的是為了更加簡單地處理原來的信號。這樣，用正餘弦來表示原信號會更加簡單，因為正餘弦擁有原信號所不具有的性質：正弦曲線保真度。且只有正弦曲線才擁有這樣的性質。
這也解釋了為什麼我們一碰到信號就想方設法的把它表示成正弦量或者復指數量的形式；為什麼方波或者三角波如此“簡單”，我們非要展開的如此“麻煩”；為什麼對於一個沒有什麼規律的“非周期”信號，我們都絞盡腦汁的用正弦量展開。就因為正弦量(或復指數)是特徵向量。
時域頻域
什麼是時域？從我們出生，我們看到的世界都以時間貫穿，股票的走勢、人的身高、汽車的軌跡都會隨著時間發生改變。這種以時間作為參照來觀察動態世界的方法我們稱其為時域分析。而我們也想當然的認為，世間萬物都在隨著時間不停的改變，並且永遠不會靜止下來。
什麼是頻域？頻域(frequency domain)是描述信號在頻率方面特性時用到的一種坐標系。用線性代數的語言就是裝著正弦函式的空間。頻域最重要的性質是：它不是真實的，而是一個數學構造。頻域是一個遵循特定規則的數學範疇。正弦波是頻域中唯一存在的波形，這是頻域中最重要的規則，即正弦波是對頻域的描述，因為時域中的任何波形都可用正弦波合成。
對於一個信號來說，信號強度隨時間的變化規律就是時域特性，信號是由哪些單一頻率的信號合成的就是頻域特性。
時域分析與頻域分析是對信號的兩個觀察面。時域分析是以時間軸為坐標表示動態信號的關係；頻域分析是把信號變為以頻率軸為坐標表示出來。一般來說，時域的表示較為形象與直觀，頻域分析則更為簡練，剖析問題更為深刻和方便。目前，信號分析的趨勢是從時域向頻域發展。然而，它們是互相聯繫，缺一不可，相輔相成的。貫穿時域與頻域的方法之一，就是傳說中的傅立葉分析。傅立葉分析可分為傅立葉級數（Fourier Serie）和傅立葉變換(Fourier Transformation)。
變換分類
根據原信號的不同類型，我們可以把傅立葉變換分為四種類別：
1非周期性連續信號傅立葉變換（Fourier Transform）
2周期性連續信號傅立葉級數(Fourier Series)
3非周期性離散信號離散時域傅立葉變換（Discrete Time Fourier Transform）
4周期性離散信號離散傅立葉變換(Discrete Fourier Transform)
下圖是四種原信號圖例：
這四種傅立葉變換都是針對正無窮大和負無窮大的信號，即信號的的長度是無窮大的，我們知道這對於計算機處理來說是不可能的，那么有沒有針對長度有限的傅立葉變換呢？沒有。因為正餘弦波被定義成從負無窮大到正無窮大，我們無法把一個長度無限的信號組合成長度有限的信號。面對這種困難，方法是把長度有限的信號表示成長度無限的信號，可以把信號無限地從左右進行延伸，延伸的部分用零來表示，這樣，這個信號就可以被看成是非周期性離解信號，我們就可以用到離散時域傅立葉變換的方法。還有，也可以把信號用複製的方法進行延伸，這樣信號就變成了周期性離散信號，這時我們就可以用離散傅立葉變換方法進行變換。這裡我們要學的是離散信號，對於連續信號我們不作討論，因為計算機只能處理離散的數值信號，我們的最終目的是運用計算機來處理信號的。
但是對於非周期性的信號，我們需要用無窮多不同頻率的正弦曲線來表示，這對於計算機來說是不可能實現的。所以對於離散信號的變換隻有離散傅立葉變換（DFT）才能被適用，對於計算機來說只有離散的和有限長度的數據才能被處理，對於其它的變換類型只有在數學演算中才能用到，在計算機面前我們只能用DFT方法，後面我們要理解的也正是DFT方法。這裡要理解的是我們使用周期性的信號目的是為了能夠用數學方法來解決問題，至於考慮周期性信號是從哪裡得到或怎樣得到是無意義的。
每種傅立葉變換都分成實數和複數兩種方法，對於實數方法是最好理解的，但是複數方法就相對複雜許多了，需要懂得有關複數的理論知識，不過，如果理解了實數離散傅立葉變換(real DFT)，再去理解複數傅立葉就更容易了，所以我們先把複數的傅立葉放到一邊去，先來理解實數傅立葉變換，在後面我們會先講講關於複數的基本理論，然後在理解了實數傅立葉變換的基礎上再來理解複數傅立葉變換。
如 上圖所示，實信號四種變換在時域和頻域的表現形式。
還有，這裡我們所要說的變換(transform)雖然是數學意義上的變換，但跟函式變換是不同的，函式變換是符合一一映射準則的，對於離散數位訊號處理（DSP），有許多的變換：傅立葉變換、拉普拉斯變換、Z變換、希爾伯特變換、離散餘弦變換等，這些都擴展了函式變換的定義，允許輸入和輸出有多種的值，簡單地說變換就是把一堆的數據變成另一堆的數據的方法。
變換意義
傅立葉變換是數位訊號處理領域一種很重要的算法。要知道傅立葉變換算法的意義，首先要了解傅立葉原理的意義。傅立葉原理表明：任何連續測量的時序或信號，都可以表示為不同頻率的正弦波信號的無限疊加。而根據該原理創立的傅立葉變換算法利用直接測量到的原始信號，以累加方式來計算該信號中不同正弦波信號的頻率、振幅和相位。
和傅立葉變換算法對應的是反傅立葉變換算法。該反變換從本質上說也是一種累加處理，這樣就可以將單獨改變的正弦波信號轉換成一個信號。因此，可以說，傅立葉變換將原來難以處理的時域信號轉換成了易於分析的頻域信號（信號的頻譜），可以利用一些工具對這些頻域信號進行處理、加工。最後還可以利用傅立葉反變換將這些頻域信號轉換成時域信號。
從現代數學的眼光來看，傅立葉變換是一種特殊的積分變換。它能將滿足一定條件的某個函式表示成正弦基函式的線性組合或者積分。在不同的研究領域，傅立葉變換具有多種不同的變體形式，如連續傅立葉變換和離散傅立葉變換。
在數學領域，儘管最初傅立葉分析是作為熱過程的解析分析的工具，但是其思想方法仍然具有典型的還原論和分析主義的特徵。"任意"的函式通過一定的分解，都能夠表示為正弦函式的線性組合的形式，而正弦函式在物理上是被充分研究而相對簡單的函式類：1. 傅立葉變換是線性運算元,若賦予適當的範數,它還是酉運算元;2. 傅立葉變換的逆變換容易求出,而且形式與正變換非常類似;3. 正弦基函式是微分運算的本徵函式,從而使得線性微分方程的求解可以轉化為常係數的代數方程的求解.線上性時不變雜的卷積運算為簡單的乘積運算,從而提供了計算卷積的一種簡單手段;4. 離散形式的傅立葉的物理系統內,頻率是個不變的性質,從而系統對於複雜激勵的回響可以通過組合其對不同頻率正弦信號的回響來獲取;5. 著名的卷積定理指出:傅立葉變換可以化復變換可以利用數字計算機快速的算出(其算法稱為快速傅立葉變換算法(FFT))。
正是由於上述的良好性質,傅立葉變換在物理學、數論、組合數學、信號處理、機率、統計、密碼學、聲學、光學等領域都有著廣泛的套用。
圖像傅立葉變換
圖像的頻率是表征圖像中灰度變化劇烈程度的指標，是灰度在平面空間上的梯度。如：大面積的沙漠在圖像中是一片灰度變化緩慢的區域，對應的頻率值很低；而對於地表屬性變換劇烈的邊緣區域在圖像中是一片灰度變化劇烈的區域，對應的頻率值較高。傅立葉變換在實際中有非常明顯的物理意義，設f是一個能量有限的模擬信號，則其傅立葉變換就表示f的譜。從純粹的數學意義上看，傅立葉變換是將一個函式轉換為一系列周期函式來處理的。從物理效果看，傅立葉變換是將圖像從空間域轉換到頻率域，其逆變換是將圖像從頻率域轉換到空間域。換句話說，傅立葉變換的物理意義是將圖像的灰度分布函式變換為圖像的頻率分布函式，傅立葉逆變換是將圖像的頻率分布函式變換為灰度分布函式。
傅立葉變換以前，圖像（未壓縮的點陣圖）是由對在連續空間（現實空間）上的採樣得到一系列點的集合，我們習慣用一個二維矩陣表示空間上各點，則圖像可由z=f(x,y)來表示。由於空間是三維的，圖像是二維的，因此空間中物體在另一個維度上的關係就由梯度來表示，這樣我們可以通過觀察圖像得知物體在三維空間中的對應關係。為什麼要提梯度？因為實際上對圖像進行二維傅立葉變換得到頻譜圖，就是圖像梯度的分布圖，當然頻譜圖上的各點與圖像上各點並不存在一一對應的關係，即使在不移頻的情況下也是沒有。傅立葉頻譜圖上我們看到的明暗不一的亮點，實際上圖像上某一點與鄰域點差異的強弱，即梯度的大小，也即該點的頻率的大小（可以這么理解，圖像中的低頻部分指低梯度的點，高頻部分相反）。一般來講，梯度大則該點的亮度強，否則該點亮度弱。這樣通過觀察傅立葉變換後的頻譜圖，也叫功率圖，我們首先就可以看出，圖像的能量分布，如果頻譜圖中暗的點數更多，那么實際圖像是比較柔和的（因為各點與鄰域差異都不大，梯度相對較小），反之，如果頻譜圖中亮的點數多，那么實際圖像一定是尖銳的，邊界分明且邊界兩邊像素差異較大的。對頻譜移頻到原點以後，可以看出圖像的頻率分布是以原點為圓心，對稱分布的。將頻譜移頻到圓心除了可以清晰地看出圖像頻率分布以外，還有一個好處，它可以分離出有周期性規律的干擾信號，比如正弦干擾，一副帶有正弦干擾，移頻到原點的頻譜圖上可以看出除了中心以外還存在以某一點為中心，對稱分布的亮點集合，這個集合就是干擾噪音產生的，這時可以很直觀的通過在該位置放置帶阻濾波器消除干擾。
另外說明以下幾點：
1、圖像經過二維傅立葉變換後，其變換係數矩陣表明：
若變換矩陣Fn原點設在中心，其頻譜能量集中分布在變換係數短陣的中心附近（圖中陰影區）。若所用的二維傅立葉變換矩陣Fn的原點設在左上角，那么圖像信號能量將集中在係數矩陣的四個角上。這是由二維傅立葉變換本身性質決定的。同時也表明一股圖像能量集中低頻區域。
2 、變換之後的圖像在原點平移之前四角是低頻，最亮，平移之後中間部分是低頻，最亮，亮度大說明低頻的能量大（幅角比較大）。
傅立葉變換的推廣
將其發展延伸，構造出了其他形式的積分變換:
從數學的角度理解積分變換就是通過積分運算，把一個函式變成另一個函式。也可以理解成是算內積，然後就變成一個函式向另一個函式的投影：
K（s，t）積分變換的核(Kernel)。當選取不同的積分域和變換核時，就得到不同名稱的積分變換。學術一點的說法是：向核空間投影，將原問題轉化到核空間。所謂核空間，就是這個空間裡面裝的是核函式。下表列出常見的變換及其核函式：
當然，選取什麼樣的核主要看你面對的問題有什麼特徵。不同問題的特徵不同，就會對應特定的核函式。把核函式作為基函式。將現在的坐標投影到核空間裡面去，問題就會得到簡化。之所以叫核，是因為這是最核心的地方。為什麼其他變換你都沒怎么聽說過而只熟悉傅立葉變換和拉普拉斯變換呢？因為復指數信號才是描述這個世界的特徵函式！
例子
一個關於實數離散傅立葉變換(Real DFT)實例
先來看一個變換實例，一個原始信號的長度是16，於是可以把這個信號分解9個餘弦波和9個正弦波（一個長度為N的信號可以分解成N/2+1個正餘弦信號，這是為什麼呢？結合下面的18個正餘弦圖,我想從計算機處理精度上就不難理解，一個長度為N的信號，最多只能有N/2+1個不同頻率，再多的頻率就超過了計算機所能所處理的精度範圍），如下圖：
9個正弦信號：
9個餘弦信號：
把以上所有信號相加即可得到原始信號，至於是怎么分別變換出9種不同頻率信號的，我們先不急，先看看對於以上的變換結果，在程式中又是該怎么表示的，我們可以看看下面這個示例圖：
上圖中左邊表示時域中的信號，右邊是頻域信號表示方法，從左向右表示正向轉換(Forward DFT)，從右向左表示逆向轉換(Inverse DFT)，用小寫x[]表示信號在每個時間點上的幅度值數組, 用大寫X[]表示每種頻率的幅度值數組, 因為有N/2+1種頻率，所以該數組長度為N/2+1，X[]數組又分兩種，一種是表示餘弦波的不同頻率幅度值：Re X[]，另一種是表示正弦波的不同頻率幅度值：Im X[]，Re是實數(Real)的意思，Im是虛數(Imagine)的意思，採用複數的表示方法把正餘弦波組合起來進行表示，但這裡我們不考慮複數的其它作用，只記住是一種組合方法而已，目的是為了便於表達（在後面我們會知道，複數形式的傅立葉變換長度是N，而不是N/2+1）。
用Matlab進行傅立葉變換
FFT是離散傅立葉變換的快速算法，可以將一個信號變換到頻域。有些信號在時域上是很難看出什麼特徵的，但是如果變換到頻域之後，就很容易看出特徵了。這就是很多信號分析採用FFT變換的原因。另外，FFT可以將一個信號的頻譜提取出來，這在頻譜分析方面也是經常用的。
FFT結果的具體物理意義。一個模擬信號，經過ADC採樣之後，就變成了數位訊號。採樣定理告訴我們，採樣頻率要大於信號頻率的兩倍。
採樣得到的數位訊號，就可以做FFT變換了。N個採樣點，經過FFT之後，就可以得到N個點的FFT結果。為了方便進行FFT運算，通常N取2的整數次方。
假設採樣頻率為Fs，信號頻率F，採樣點數為N。那么FFT之後結果就是一個為N點的複數。每一個點就對應著一個頻率點。這個點的模值，就是該頻率值下的幅度特性。具體跟原始信號的幅度有什麼關係呢？假設原始信號的峰值為A，那么FFT的結果的每個點（除了第一個點直流分量之外）的模值就是A的N/2倍。而第一個點就是直流分量，它的模值就是直流分量的N倍。而每個點的相位呢，就是在該頻率下的信號的相位。第一個點表示直流分量（即0Hz），而最後一個點N的再下一個點（實際上這個點是不存在的，這裡是假設的第N+1個點，也可以看做是將第一個點分做兩半分，另一半移到最後）則表示採樣頻率Fs，這中間被N-1個點平均分成N等份，每個點的頻率依次增加。例如某點n所表示的頻率為：Fn=(n-1)*Fs/N。由上面的公式可以看出，Fn所能分辨到頻率為為Fs/N，如果採樣頻率Fs為1024Hz，採樣點數為1024點，則可以分辨到1Hz。1024Hz的採樣率採樣1024點，剛好是1秒，也就是說，採樣1秒時間的信號並做FFT，則結果可以分析到1Hz，如果採樣2秒時間的信號並做FFT，則結果可以分析到0.5Hz。如果要提高頻率分辨力，則必須增加採樣點數，也即採樣時間。頻率解析度和採樣時間是倒數關係。
假設FFT之後某點n用複數a+bi表示，那么這個複數的模就是An=根號a*a+b*b，相位就是Pn=atan2(b,a)。根據以上的結果，就可以計算出n點（n≠1，且n<=N/2）對應的信號的表達式為：An/(N/2)*cos(2*pi*Fn*t+Pn)，即2*An/N*cos(2*pi*Fn*t+Pn)。對於n=1點的信號，是直流分量，幅度即為A1/N。由於FFT結果的對稱性，通常我們只使用前半部分的結果，即小於採樣頻率一半的結果。
下面以一個實際的信號來做說明。假設我們有一個信號，它含有2V的直流分量，頻率為50Hz、相位為-30度、幅度為3V的交流信號，以及一個頻率為75Hz、相位為90度、幅度為1.5V的交流信號。用數學表達式就是如下：S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)。式中cos參數為弧度，所以-30度和90度要分別換算成弧度。我們以256Hz的採樣率對這個信號進行採樣，總共採樣256點。按照我們上面的分析，Fn=(n-1)*Fs/N，我們可以知道，每兩個點之間的間距就是1Hz，第n個點的頻率就是n-1。我們的信號有3個頻率：0Hz、50Hz、75Hz，應該分別在第1個點、第51個點、第76個點上出現峰值，其它各點應該接近0。實際情況如何呢？我們來看看FFT的結果的模值如圖所示。
從圖中我們可以看到，在第1點、第51點、和第76點附近有比較大的值。我們分別將這三個點附近的數據拿上來細看：
1點： 512+0i
2點： -2.6195E-14 - 1.4162E-13i
3點： -2.8586E-14 - 1.1898E-13i
50點：-6.2076E-13 - 2.1713E-12i
51點：332.55 - 192i
52點：-1.6707E-12 - 1.5241E-12i
75點：-2.2199E-13 -1.0076E-12i
76點：3.4315E-12 + 192i
77點：-3.0263E-14 +7.5609E-13i
很明顯，1點、51點、76點的值都比較大，它附近的點值都很小，可以認為是0，即在那些頻率點上的信號幅度為0。接著，我們來計算各點的幅度值。分別計算這三個點的模值，結果如下：
1點： 512
51點：384
76點：192
按照公式，可以計算出直流分量為：512/N=512/256=2；50Hz信號的幅度為：384/(N/2)=384/(256/2)=3；75Hz信號的幅度為192/(N/2)=192/(256/2)=1.5。可見，從頻譜分析出來的幅度是正確的。
然後再來計算相位信息。直流信號沒有相位可言，不用管它。先計算50Hz信號的相位，atan2(-192, 332.55)=-0.5236,結果是弧度，換算為角度就是180*(-0.5236)/pi=-30.0001。再計算75Hz信號的相位，atan2(192, 3.4315E-12)=1.5708弧度，換算成角度就是180*1.5708/pi=90.0002。可見，相位也是對的。根據FFT結果以及上面的分析計算，我們就可以寫出信號的表達式了，它就是我們開始提供的信號。
總結：假設採樣頻率為Fs，採樣點數為N，做FFT之後，某一點n（n從1開始）表示的頻率為：Fn=(n-1)*Fs/N；該點的模值除以N/2就是對應該頻率下的信號的幅度（對於直流信號是除以N）；該點的相位即是對應該頻率下的信號的相位。相位的計算可用函式atan2(b,a)計算。atan2(b,a)是求坐標為(a,b)點的角度值，範圍從-pi到pi。要精確到xHz，則需要採樣長度為1/x秒的信號，並做FFT。要提高頻率解析度，就需要增加採樣點數，這在一些實際的套用中是不現實的，需要在較短的時間內完成分析。解決這個問題的方法有頻率細分法，比較簡單的方法是採樣比較短時間的信號，然後在後面補充一定數量的0，使其長度達到需要的點數，再做FFT，這在一定程度上能夠提高頻率分辨力。具體的頻率細分法可參考相關文獻。
套用
儘管最初傅立葉分析是作為熱過程的解析分析的工具，但是其思想方法仍然具有典型的還原論和分析主義的特徵。"任意"的函式通過一定的分解，都能夠表示為正弦函式的線性組合的形式，而正弦函式在物理上是被充分研究而相對簡單的函式類，這一想法跟化學上的原子論想法何其相似！奇妙的是，現代數學發現傅立葉變換具有非常好的性質，使得它如此的好用和有用，讓人不得不感嘆造物的神奇：
- 傅立葉變換是線性運算元，若賦予適當的範數，它還是酉運算元；
- 傅立葉變換的逆變換容易求出，而且形式與正變換非常類似；
- 著名的卷積定理指出：傅立葉變換可以化複雜的卷積運算為簡單的乘積運算，從而提供了計算卷積的一種簡單手段；
- 離散形式的傅立葉變換可以利用數字計算機快速的算出（其算法稱為快速傅立葉變換算法（FFT)).
正是由於上述的良好性質，傅立葉變換在物理學、數論、組合數學、信號處理、機率、統計、密碼學、聲學、光學等領域都有著廣泛的套用。
有關傅立葉變換的FPGA實現
傅立葉變換是數位訊號處理中的基本操作，廣泛套用於表述及分析離散時域信號領域。但由於其運算量與變換點數N的平方成正比關係，因此，在N較大時，直接套用DFT算法進行譜變換是不切合實際的。然而，快速傅立葉變換技術的出現使情況發生了根本性的變化。本文主要描述了採用FPGA來實現2k/4k/8k點FFT的設計方法。
整體結構
一般情況下，N點的傅立葉變換對為：
N=8192點DFT的運算表達式為：
式中，m=(4n1+n2)(2048k1+k2)(n=4n1+n2，k=2048k1+k2）其中n1和k2可取0,1，．．．，2047,k1和n2可取0,1,2,3。
由式（3）可知，8k傅立葉變換可由4×2k的傅立葉變換構成。同理，4k傅立葉變換可由2×2k的傅立葉變換構成。而2k傅立葉變換可由128×16的傅立葉變換構成。128的傅立葉變換可進一步由16×8的傅立葉變換構成，歸根結底，整個傅立葉變換可由基2、基4的傅立葉變換構成。2k的FFT可以通過5個基4和1個基2變換來實現；4k的FFT變換可通過6個基4變換來實現；8k的FFT可以通過6個基4和1個基2變換來實現。也就是說：FFT的基本結構可由基2/4模組、複數乘法器、存儲單元和存儲器控制模組構成，其整體結構如圖1所示。
圖1中，RAM用來存儲輸入數據、運算過程中的中間結果以及運算完成後的數據，ROM用來存儲旋轉因子表。蝶形運算單元即為基2/4模組，控制模組可用於產生控制時序及地址信號，以控制中間運算過程及最後輸出結果。
蝶形運算器
基4和基2的信號流如圖2所示。圖中，若A=r0+j*i0，B=r1+j*i1，C=r2+j*i2，D=r3+j*i3是要進行變換的信號，Wk0=c0+j*s0=1，Wk1=c1+j*s1，Wk2=c2+j*s2，Wk3=c3+j*s3為旋轉因子，將其分別代入圖2中的基4蝶形運算單元，則有：
A′=[r0+(r1×c1－i1×s1)+(r2×c2－i2×s2)+(r3×c3－i3×s3)]+j[i0+(i1×c1+r1×s1)+(i2×c2+r2×s2)+(i3×c3+r3×s3)]? （4）
B′=[r0+(i1×c1+r1×s1）－（r2×c2－i2×s2）－（i3×c3+r3×s3)]+j[i0－（r1×c1－i1×s1）－（i2×c2+r2×s2)+(r3×c3－i3×s3)] (5）
C′=[r0－（r1×c1－i1×s1)+(r2×c2－i2×s2）－（r3×c3－i3×s3)]+j[i0－（i1×c1+r1×s1)+(i2×c2+r2×s2）－（i3×c3+r3×s3)] （6）
D′=[r0－（i1×c1+r1×s1）－（r2×c2－i2×s2)+(i3×c3+r3×s3)]+j[i0+(r1×c1－i1×s1）－（i2×c2+r2×s2）－（r3×c3－i3×s3)]? （7）
而在基2蝶形中，Wk0和Wk2的值均為1，這樣，將A，B，C和D的表達式代入圖2中的基2運算的四個等式中，則有：
A′=r0+(r1×c1－i1×s1)+j[i0+(i1×c1+r1×s1)]? （8）
B′=r0－ (r1×c1－i1×s1)+j[i0－（i1×c1+r1×s1)] （9）
C′=r2+(r3×c3－i3×s3)+j[i0+(i3×c3+r3×s3)]? （10）
D′=r2－（r3×c3－i3×s3)+j[i0－（i3×c3+r3×s3)]? （11）
在上述式（4）～（11）中有很多類同項，如i1×c1+r1×s1和r1×c1－i1×s1等，它們僅僅是加減號的不同，其結構和運算均類似，這就為簡化電路提供了可能。同時，在蝶形運算中，複數乘法可以由實數乘法以一定的格式來表示，這也為設計複數乘法器提供了一種實現的途徑。
以基4為例，在其運算單元中，實際上只需做三個複數乘法運算，即只須計算BWk1、CWk2和DWk3的值即可，這樣在一個基4蝶形單元裡面，最多只需要3個複數乘法器就可以了。在實際過程中，在不提高時鐘頻率下，只要將時序控制好?便可利用流水線（Pipeline）技術並只用一個複數乘法器就可完成這三個複數乘法，大大節省了硬體資源。
圖2 基2和基4蝶形算法的信號流圖
FFT的地址
FFT變換後輸出的結果通常為一特定的倒序。因此，幾級變換後對地址的控制必須準確無誤。
倒序的規律是和分解的方式密切相關的，以基8為例，其基本倒序規則如下：
基8可以用2×2×2三級基2變換來表示，則其輸入順序則可用二進制序列（n1 n2 n3）來表示，變換結束後，其順序將變為（n3 n2 n1），如：X?011 → x?110 ，即輸入順序為3，輸出時順序變為6。
更進一步，對於基16的變換，可由2×2×2×2，4×4，4×2×2等形式來構成，相對於不同的分解形式，往往會有不同的倒序方式。以4×4為例，其輸入順序可以用二進制序列（n1 n2 n3n4）來表示變換結束後，其順序可變為（（n3 n4）（n1 n2）），如：X?0111 → x?1101 。即輸入順序為7，輸出時順序變為13。
在2k/4k/8k的傅立葉變換中，由於要經過多次的基4和基2運算，因此，從每次運算完成後到進入下一次運算前，應對運算的結果進行倒序，以保證運算的正確性。
旋轉因子
N點傅立葉變換的旋轉因子有著明顯的周期性和對稱性。其周期性表現為：
FFT之所以可使運算效率得到提高，就是利用了對稱性和周期性把長序列的DFT逐級分解成幾個序列的DFT，並最終以短點數變換來實現長點數變換。
根據旋轉因子的對稱性和周期性，在利用ROM存儲旋轉因子時，可以只存儲旋轉因子表的一部分，而在讀出時增加讀出地址及符號的控制，這樣可以正確實現FFT。因此，充分利用旋轉因子的性質，可節省70%以上存儲單元。
實際上，由於旋轉因子可分解為正、餘弦函式的組合，故ROM中存的值為正、餘弦函式值的組合。對2k/4k/8k的傅立葉變換來說，只是對一個周期進行不同的分割。由於8k變換的旋轉因子包括了2k/4k的所有因子，因此，實現時只要對讀ROM的地址進行控制，即可實現2k/4k/8k變換的通用。
存儲器控制
因FFT是為時序電路而設計的，因此，控制信號要包括時序的控制信號及存儲器的讀寫地址，並產生各種輔助的指示信號。同時在計算模組的內部，為保證高速，所有的乘法器都須始終保持較高的利用率。這意味著在每一個時鐘來臨時都要向這些單元輸入新的運算元，而這一切都需要控制信號的緊密配合。
為了實現FFT的流形運算，在運算的同時，存儲器也要接收數據。這可以採用桌球RAM的方法來完成。這種方式決定了實現FFT運算的最大時間。對於4k操作，其接收時間為4096個數據周期,這樣FFT的最大運算時間就是4096個數據周期。另外，由於輸入數據是以一定的時鐘為周期依次輸入的，故在進行內部運算時，可以用較高的內部時鐘進行運算，然後再存入RAM依次輸出。
為節省資源，可對存儲數據RAM採用原址讀出原址寫入的方法，即在進行下一級變換的同時，首先應將結果回寫到讀出數據的RAM存貯器中；而對於ROM，則應採用與運算的數據相對應的方法來讀出存儲器中旋轉因子的值。
在2k/4k/8k傅立葉變換中，要實現通用性，控制器是最主要的模組。2k、4k、8k變換具有不同的內部運算時間和存儲器地址，在設計中，針對不同的點數應設計不同的存儲器存取地址，同時，在完成變換後，還要對開始輸出有用信號的時刻進行指示。
