基本介紹
- 中文名:傅立葉級數
- 外文名:Fourier series
- 提出者:傅立葉
- 適用領域範圍:任何周期函式
- 性質:一種特殊的三角級數
- 套用學科:數學
來源
 傅立葉級數
傅立葉級數公式
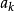
 傅立葉級數
傅立葉級數性質
收斂性
 傅立葉級數
傅立葉級數正交性
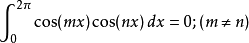

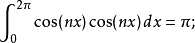
 傅立葉級數
傅立葉級數奇偶性
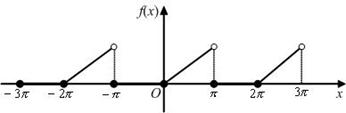 傅立葉級數
傅立葉級數廣義傅立葉級數
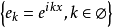
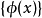
 傅立葉級數
傅立葉級數
 傅立葉級數
傅立葉級數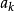
 傅立葉級數
傅立葉級數 傅立葉級數
傅立葉級數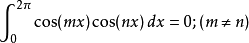

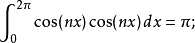
 傅立葉級數
傅立葉級數 傅立葉級數
傅立葉級數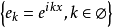
 傅立葉級數
傅立葉級數法國數學家傅立葉發現,任何周期函式都可以用正弦函式和餘弦函式構成的無窮級數來表示(選擇正弦函式與餘弦函式作為基函式是因為它們是正交的),後世稱傅立葉級數為一...
傅立葉展開式(Fourier expansion)是指用三角級數表示的形式,即一個函式的傅立葉級數在它收斂於此函式本身時的一種稱呼。若函式f(x)的傅立葉級數處處收斂於f (...
傅立葉係數由Fourier coefficient 翻譯而來,有多箇中文譯名。它是數學分析中的一個概念,常常被套用在信號處理領域中。對於任意的周期信號,如果滿足一定條件,都可以...
廣義傅立葉級數(generalized Fourier series)是特殊的正交級數,函式f(r)在區間[0,a]上具有二階連續導數,則f(r)可以展開成以貝塞爾函式為基的廣義傅立葉級數。...
傅立葉級數是一類特殊的三角級數。當n≥2時,常稱σ(f)為多重傅立葉級數。...... 傅立葉級數是一類特殊的三角級數。當n≥2時,常稱σ(f)為多重傅立葉級數...
連續形式的傅立葉變換其實是傅立葉級數的推廣,因為積分其實是一種極限形式的求和運算元而已。對於周期函式,它的傅立葉級數(Fourier series)表示被定義為:...
讓·巴普蒂斯·約瑟夫·傅立葉(Baron Jean Baptiste Joseph Fourier,1768-1830),男爵,法國數學家、物理學家,1768年3月21日生於歐塞爾,1830年5月16日卒於巴黎。...
在單變元情形,常把傅立葉級數σ(f)寫成實形式,其中的ak稱為f的餘弦傅立葉係數。...... 在單變元情形,常把傅立葉級數σ(f)寫成實形式,其中的ak稱為f的...
傅氏級數即傅立葉級數。法國數學家傅立葉發現,任何周期函式都可以用正弦函式和餘弦函式構成的無窮級數來表示(選擇正弦函式與餘弦函式作為基函式是因為它們是正交的)...
《現代傅立葉分析》是2011年出版的圖書,作者是格拉法克斯。...... 《現代傅立葉分析》是2011年出版的圖書,作者...傅立葉級數、傅立葉變換、極大值函式、奇異...
傅立葉級數的部分和的簡稱。...... 級數正文設。詞條標籤: 文化 圖集 傅立葉和圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:5次歷史版本 最近更新: ...
傅立葉分析Fourier analysis 分析學中18世紀逐漸形成的一個重要分支,主要研究函式的傅立葉變換及其性質。又稱調和分析。在經歷了近2個世紀的發展之後,研究領域已從...
約瑟夫·傅立葉,全稱為讓·巴普蒂斯·約瑟夫·傅立葉(Jean Baptiste Joseph Fourier,1768年3月21日生於法國榮納省歐塞爾,1830年5月16日卒於法國巴黎),法國數學家...
Fourier分析,即傅立葉分析,是數學的一個分支領域。它研究如何將一個函式或者信號表達為基本波形的疊加。它研究並擴展傅立葉級數和傅立葉變換的概念。基本波形稱為...
特點 具有三維周期性的晶體結構對應的晶體電子密度函式p ( .r,,,:)可用止交、歸一的正弦、餘弦函式組或正交、歸一的指數函式組進行傅立葉級數展開,當選擇指數...
《傅立葉原理》是一款Android平台的套用。...... 傅立葉原理套用介紹 編輯 歡迎傅立葉原則。現在,通過總結三角波功能,可以近似的原則和機制的傅立葉級數,我們可以...
級數是指將數列的項依次用加號連線起來的函式。典型的級數有正項級數、交錯級數、冪級數、傅立葉級數等。級數理論是分析學的一個分支;它與另一個分支微積分學一...
《漫畫傅立葉解析》是2009年8月1日科學出版社出版的圖書,作者是涉谷道雄,漫畫繪製是HaruseHiroki,漫畫編制是株式會社TRENO-PRO,翻譯是陳芳。...
DFS也即離散傅立葉級數,又稱離散時間傅立葉級數即DTFS,T代表時間。... DFS也即離散傅立葉級數,又稱離散時間傅立葉級數即DTFS,T代表時間。 中文名 離散傅立葉...
