基本介紹
- 中文名:廣義傅立葉級數
- 外文名:generalized Fourier series
- 所屬學科:數學
- 簡介:一種特殊的正交級數
- 相關概念:貝塞爾(Bessel)函式
基本介紹




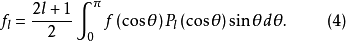
例題解析





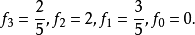






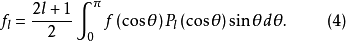





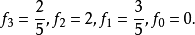

廣義傅立葉級數(generalized Fourier series)是特殊的正交級數,函式f(r)在區間[0,a]上具有二階連續導數,則f(r)可以展開成以貝塞爾函式為基的廣義傅立葉級數。...
法國數學家傅立葉發現,任何周期函式都可以用正弦函式和餘弦函式構成的無窮級數來表示(選擇正弦函式與餘弦函式作為基函式是因為它們是正交的),後世稱傅立葉級數為一...
傅立葉展開式(Fourier expansion)是指用三角級數表示的形式,即一個函式的傅立葉級數在它收斂於此函式本身時的一種稱呼。若函式f(x)的傅立葉級數處處收斂於f (...
Fourier分析,即傅立葉分析,是數學的一個分支領域。它研究如何將一個函式或者信號表達為基本波形的疊加。它研究並擴展傅立葉級數和傅立葉變換的概念。基本波形稱為...
4 連帶勒讓德函式的母函式 5 連帶勒讓德函式的遞推公式 6 連帶勒讓德函式的正交歸一性 7 連帶勒讓德函式的廣義傅立葉級數展開 連帶...
16.2.2 勒讓德多項式的套用(廣義傅立葉級數展開) 30316.3 勒讓德多項式的生成函式(母函式) 30516.3.1 勒讓德多項式的生成函式的定義305...
4.3.4 廣義傅立葉級數展開4.4 勒讓德多項式在解數理方程中的套用4.5 連帶勒讓德函式4.5.1 連帶勒讓德函式本徵值問題4.5.2 連帶勒讓德函式的性質...
10.2.6廣義傅立葉級數10.3虛宗量貝塞爾函式10.3.1虛宗量貝塞爾方程10.3.2虛宗量貝塞爾函式的表達式10.3.3虛宗量貝塞爾函式的性質...
習題2第3章 泰勒級數、羅朗級數和留數3.1 泰勒級數和羅朗級數3.2 孤立奇點和留數3.3 留數與積分的關係習題3第4章 傅立葉變換4.1 正交函式系與廣義函式...
