DFS也即離散傅立葉級數,又稱離散時間傅立葉級數即DTFS,T代表時間。
基本介紹
- 中文名:離散傅立葉級數
- 外文名:discrete-time Fourier series
- 類型:公式
- 特點:周期性,離散性
簡介
級數公式
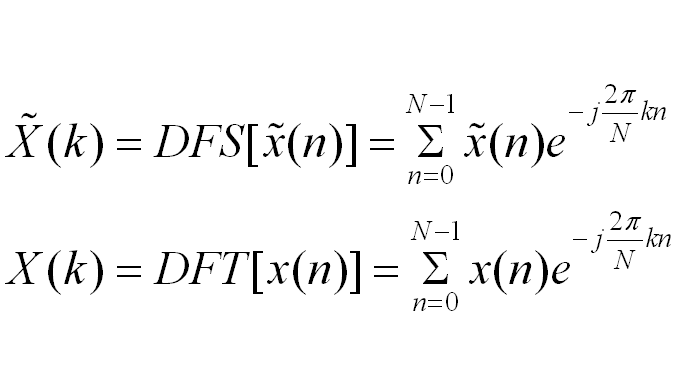

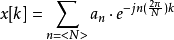

進一分析
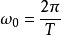
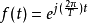





DFS也即離散傅立葉級數,又稱離散時間傅立葉級數即DTFS,T代表時間。
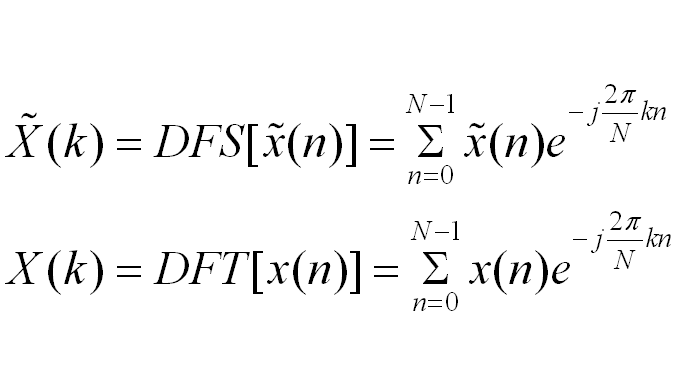

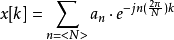

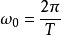
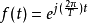




DFS也即離散傅立葉級數,又稱離散時間傅立葉級數即DTFS,T代表時間。... DFS也即離散傅立葉級數,又稱離散時間傅立葉級數即DTFS,T代表時間。 中文名 離散傅立葉...
DFS是一個奢侈品旅遊零售商。自1960年於香港成立,其免稅店網路已包括18個主要國際機場及14個市區T廣場店鋪,同時其附屬及度假村據點亦遍布全球。集團為私營企業並由...
DFS(Dutyfreeshoppers)集團是成立於1961的全球首屈一指的免稅企業,是世界最大的旅遊業零售集團和世界最大的機場免稅經營者,目前其在亞太區14個國家和北美東海岸...
FastDFS是一個開源的輕量級分散式檔案系統,它對檔案進行管理,功能包括:檔案存儲、檔案同步、檔案訪問(檔案上傳、檔案下載)等,解決了大容量存儲和負載均衡的問題。特別...
Microsoft檔案分布系統 (Dfs) 是一個網路伺服器組件,它能夠使你更容易地在網路上查詢和管理數據。分散式檔案系統是將分布於不同電腦上的檔案組合為單一的名稱空間,...
DFS環球免稅店是一家擁有13家大型一站式精品商城,成立於1995年,占地面積約2,000平方米到16,000平方米。匯集世界著名、受歡迎的名牌精品。這裡既有眾所周知的資深...
澳門DFS環球免稅店是DFS集團成員之一,位於澳門路氹金光大道。...... 在澳門DFS [2] ,可以找到眾多大牌為DFS獨家定製專售的限量精品和最新最熱的時尚名品。顧客享受...
1960年11月7日,兩個美國企業家,Charles Feeney 與 Robert Miller創立了DFS環球免稅店 DFS Group LTD 成立時間: 1961年 主營: 國際遊客商品零售商 525 Market ...
塞班島DFS環球免稅店是塞班島最大、歷史最悠久的購物中心,占地約100,000平方英尺。DFS(Duty Free Shoppers)環球免稅集團是全球最大的免稅店運營商,一直致力於為...
DFS(Duty Free Shoppers)環球免稅集團是全球最大的免稅店運營商,一直致力於為國際旅行者提供世界頂級品牌精品、優惠價格以及百分百環球保證服務。...
澳大利亞除了是旅行勝地,更加是購物的好地方!全球最大的DFS環球免稅店在澳大利亞開設三家分店,分別在凱恩斯、悉尼和黃金海岸。在這裡您可以享受一站式奢華購物體驗,以...
香港素有“購物天堂”的美稱,商品款式新穎齊全、選擇多元化,而且價格豐儉由人,在那裡購物,樂趣無窮。出徵購物到香港DFS環球免稅店當仁不讓地成為最重要的目的地,在...
新加坡DFS環球免稅店坐落於烏節購物區最繁華的史格士路上。樓高四層的新加坡DFS,包羅國際知名品牌,女士鐘愛的化妝品、珠寶,男士必選的腕錶、名牌箱包及菸酒,甚至...
紐西蘭DFS免稅店位於奧克蘭Custom街和Albert街交界處,占地面積達50,000平方米,店內有奧克蘭品種最齊全的化妝品、香水和頂級名牌商品,DFS獨家銷售的限量版商品以及當地...
DFS是Distributed File System (分散式檔案處理)縮寫,DFS為用戶提供訪問分布在網路中的已分享檔案夾的便捷途徑。DFS是一個單獨的、邏輯的、層次的檔案系統。它將同一...
DFS 外文名 disease free survival 特點 統計癌症病人的存活率 性質 統計指標 disease free survival醫學界為了統計癌症病人的存活率,採用的統計指標V...
巴厘島免稅店(DFS Galleria)位於Kuta。DFS是巴厘島最大的商店,有最多品種的名牌商品可供選購。
夏威夷DFS環球免稅店位於動感時尚的懷基基海灘,是夏威夷政府唯一認可的免稅零售商,也是全島最大的奢華購物聖地。...
DFS(動態頻率選擇)編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!Dynamic frequency selection 是一種用於動態選擇無線...
2004年5月20日,DFS(中國)有限責任公司成立,並以其穩重的發展態勢,展示著一個化妝品批發領先者的強大魅力。...
澳門DFS環球免稅店位於澳門四季酒店一層,毗鄰路氹金光大道,占地 110,000平方尺的輝煌店面內,匯集超過110個全球頂級奢華品牌。在這裡,您能找到眾多大牌為DFS獨家定製...
DFS-R。 DFS-R 是一種強大的多主機檔案複製服務,在檔案伺服器同步的可伸縮性和效率方面,都大大優於其前身檔案複製服務 (FRS)。DFS-R 可用於將分支機構數據,...
DFS環球免稅店匯集世界最著名、最受歡迎的名牌精品,既有眾所周知的資深大牌如Cartier卡地亞、Chanel香奈爾、Gucci古馳Louis Vuitton路易威登和Tiffany蒂芙尼,也有新興時尚...
從1995年在關島開業的第一家DFS環球免稅 店,到2008在澳門最新開幕的萬餘平米新店,市內點一直是DFS成功的要素。 迄今,DFS共擁有13家大型一站式精品商城—DFS環球...
DFS是多義詞,共8個義項 展開 科普中國 本詞條由“科普中國”百科科學詞條編寫與套用工作項目審核 深度優先搜尋是一種在開發爬蟲早期使用較多的方法。它的目的是...
日本環球免稅店特指開設在日本沖繩島那霸的沖繩島DFS環球免稅店。總面積達45,000平方米,交通便利,購物環境奢華、高雅、藝術,日本環球免稅店為前往沖繩島旅遊的遊客...
