基本介紹
- 中文名:離散時間傅立葉變換
- 外文名:Discrete-time Fourier Transform
- 別稱:DTFT
- 提出者:傅立葉
定義


性質
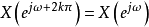



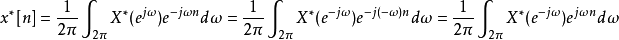






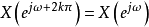



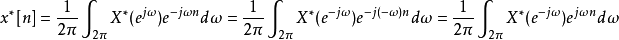




離散時間傅立葉變換(英語:Discrete-time Fourier Transform,簡稱:DTFT)是傅立葉變換的一種。它將以離散時間nT(其中,T為採樣間隔)作為變數的函式(離散時間信號)...
離散傅立葉變換(Discrete Fourier Transform,DFT)傅立葉分析方法是信號分析的最基本方法,傅立葉變換是傅立葉分析的核心,通過它把信號從時間域變換到頻率域,進而...
離散時間非周期序列的傅立葉變換,把一個非周期的時間序列用連續頻率的周期函式表示的一種變換方法。...
領域,傅立葉變換具有多種不同的變體形式,如連續傅立葉變換和離散傅立葉變換...為方便起見,本文統一寫作“傅立葉變換”。傅立葉變換是一種分析信號的方法,它...
離散傅立葉級數,連續周期信號的連續傅立葉級數有著無窮多的離散頻率分量,相鄰分量的間距由信號的周期決定,等於1/T(角度,弧度乘2π)。...
《離散時間信號分析和處理》是2001年清華大學出版社出版的圖書,作者是應啟珩、...2 時域離散信號――序列 3 序列的z變換 …… 第2章 離散傅立葉變換(DFT) ...
60年代計算機科學的發展與套用是離散時間系統的理論研究和實踐進入一個新階段。1965年庫利(J.W.Cooley)和圖基(J.W.Tukey)—發明FFT快速傅立葉變換。同時,超大...
快速傅立葉變換 (fast Fourier transform), 即利用計算機計算離散傅立葉變換(DFT)的高效、快速計算方法的統稱,簡稱FFT。快速傅立葉變換是1965年由J.W.庫利和T....
《快速傅立葉變換及其C程式》是中國科學技術大學出版社出版的。本書系統地介紹了傅立葉變換的理論和技術,內容包括傅立葉變換(FT)的定義、存在條件及其性質,離散傅...
時域離散信號系統是輸入與輸出均為時域離散信號的系統,本質上即處理時域離散信號...均屬於時域離散信號系統,包括快速傅立葉變換,頻域或時域的增強處理,分析與合成,...
Z變換(英文:z-transformation)可將時域信號(即:離散時間序列)變換為在復頻域的...Z變換是傅立葉變換的推廣,當傅立葉變換不存在時,Z變換所定義的冪級數可能收斂...
DTFT,離散時間傅立葉變換(DTFT,Discrete-time Fourier Transform),是傅立葉變換的一種。也可以叫做序列的傅立葉變換...
短時傅立葉變換(STFT)是和傅立葉變換相關的一種數學變換,用以確定時變信號其局部區域正弦波的頻率與相位。...
