stft

短時傅立葉變換（STFT）是和傅立葉變換相關的一種數學變換，用以確定時變信號其局部區域正弦波的頻率與相位。

基本介紹

• 中文名：短時傅立葉變換
• 外文名：Short-Time Fourier Transform
• 簡稱：ＳＴＦＴ

問題的提出

起初，在信號學裡面，為了簡化運算，尤其是線上性時不變系統（LTI，linear time invariance system）中的運算，從而引入了傅立葉變換的概念。然而傅立葉變換隻能夠給出信號的頻域性質。也就是說頻率並沒有對應到時間上。這對於一個穩定信號是沒有什麼影響的，因為信號的頻率永遠都是一種分布。然而對於一個非穩定的信號，由於頻率隨時間在變化，那么使用傅立葉變換就無法完整的描述這種變化的性質。為了更好地表達這種變化的特點，短時傅立葉變換（STFT）被引入並且很快得到了推廣。

短時傅立葉變換分為兩種，分別對應到連續時間和離散時間上。

變換公式

連續時間短時傅立葉變換

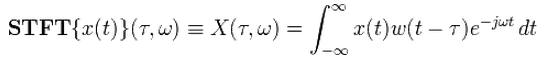
x（t）代表信號，w（t）是窗函式。

離散時間短時傅立葉變換

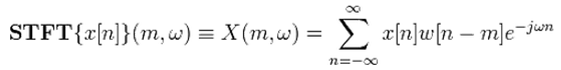
x【n】代表信號，w【n】是窗函式。

事實上，離散的形式是連續的一種採樣方式。

此外，我們常見的聲音頻譜圖就是使用stft繪製而成的，其實質就是stft的能量，也就是模值的平方。

STFT的解析度

STFT的使用範圍受其變換性質的局限。STFT是一種基於窗函式的變換，一般來說，短窗能夠提供較好的時域解析度，長窗能夠提供較好的頻域解析度。這導致其實在研究過程中，還是只能側重一種研究角度，或稱一種側重的解析度。所以這並不是多解析度分析。這也是為什麼之後又提出了小波變換的原因之一。

不過，總體來說，STFT對於大部分音頻信號都能夠有較好的的分析效果，所以還是一種在使用的分析方法。