在數學中,連續傅立葉變換是一個特殊的把一組函式映射為另一組函式的線性運算元。 不嚴格地說,傅立葉變換就是把一個函式分解為組成該函式的連續頻率譜。 在數學分析中,信號f(t)的傅立葉變換被認為是處在頻域中的信號。 這一基本思想類似於其他傅立葉變換,如周期函式的傅立葉級數。(參見分數階傅立葉變換得到概況)
基本介紹
- 中文名:連續傅立葉變換
- 不嚴格地說:把一個函式分解為該函式的頻率譜
- 特殊情況:傅立葉坐標有時可用來代替
- 舉例:假設是一個復勒貝格可積的函式
舉例

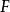

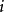
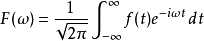
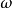
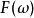
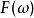


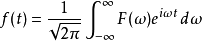
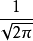
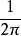


特殊情況



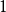

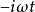
在數學中,連續傅立葉變換是一個特殊的把一組函式映射為另一組函式的線性運算元。 不嚴格地說,傅立葉變換就是把一個函式分解為組成該函式的連續頻率譜。 在數學分析中,信號f(t)的傅立葉變換被認為是處在頻域中的信號。 這一基本思想類似於其他傅立葉變換,如周期函式的傅立葉級數。(參見分數階傅立葉變換得到概況)

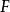

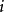
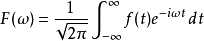
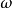
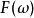
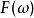


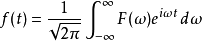
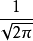
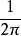





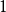

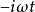
在數學中,連續傅立葉變換是一個特殊的把一組函式映射為另一組函式的線性運算元。 不嚴格地說,傅立葉變換就是把一個函式分解為組成該函式的連續頻率譜。 在數學...
傅立葉變換,表示能將滿足一定條件的某個函式表示成三角函式(正弦和/或餘弦函式)或者它們的積分的線性組合。在不同的研究領域,傅立葉變換具有多種不同的變體形式...
連續視窗傅立葉變換亦稱短時傅立葉變換,它是在傅立葉變換積分表達式的被積函式之中加上一個視窗函式而成的。...
離散傅立葉變換(Discrete Fourier Transform,DFT)傅立葉分析方法是信號分析的最基本方法,傅立葉變換是傅立葉分析的核心,通過它把信號從時間域變換到頻率域,進而...
離散時間傅立葉變換(英語:Discrete-time Fourier Transform,簡稱:DTFT)是傅立葉變換的一種。它將以離散時間nT(其中,T為採樣間隔)作為變數的函式(離散時間信號)...
傅立葉變換(Fourier transform ) 傅立葉變換能將滿足一定條件的某個函式表示成三角函式(正弦和/或餘弦函式)或者它們的積分的線性組合。在不同的研究領域,傅立葉...
儘管傅立葉變換及其離散形式DFT已經成為信號處理,尤其是時頻分析中最常用的工具,但是,傅立葉變換存在信號的時域與頻域信息不能同時局部化的問題。故Dennis Gabor於...
讓·巴普蒂斯·約瑟夫·傅立葉(Baron Jean Baptiste Joseph Fourier,1768-1830),男爵,法國數學家、物理學家,1768年3月21日生於歐塞爾,1830年5月16日卒於巴黎。...
核磁共振儀按掃描方式不同可分為兩大類———連續波核磁共振儀和脈衝傅立葉變換 核磁共振儀。脈衝傅立葉變換共振實驗脈衝時間短,每次脈衝的時間間隔一般僅為幾秒...
《快速傅立葉變換及其C程式》是中國科學技術大學出版社出版的。本書系統地介紹了傅立葉變換的理論和技術,內容包括傅立葉變換(FT)的定義、存在條件及其性質,離散傅...
離散分數傅立葉變換是用來解決數字序列分數傅立葉變換的計算問題,方法是利用它們的特徵函式展開的表達來實現離散算法。...
傅立葉反演公式是經典傅立葉公式的推廣。在數學中,傅立葉反演定理說,對於許多類型的函式,可以從其傅立葉變換中得到原函式。 直觀地,它可以被視為,如果我們知道...
離散時間非周期序列的傅立葉變換,把一個非周期的時間序列用連續頻率的周期函式表示的一種變換方法。...
約瑟夫·傅立葉,全稱為讓·巴普蒂斯·約瑟夫·傅立葉(Jean Baptiste Joseph Fourier,1768年3月21日生於法國榮納省歐塞爾,1830年5月16日卒於法國巴黎),法國數學家...
《傅立葉變換紅外光譜分析(第2版)》出版社: 化學工業出版社 本書系統地介紹了紅外光譜的基本概念、傅立葉變換紅外光譜學的基本原理、傅立葉變換紅外光譜儀的結構...
當一個非常複雜的函式變成多個初等正弦函式相加時,它的積分比之前對複雜函式的積分變得簡單多了。法國數學家傅立葉發現了周期函式可以用一系列正弦函式組成的級數...
核磁共振儀按掃描方式不同可分為兩大類——連續波核磁共振儀和脈衝傅立葉變換 核磁共振儀。核磁共振儀是由磁鐵、探頭、射頻發生器、射頻接收器、掃描發生器、信號...
短時傅立葉變換(STFT)是和傅立葉變換相關的一種數學變換,用以確定時變信號其局部區域正弦波的頻率與相位。...
離散傅立葉變換(Discrete Fourier Transform,縮寫為DFT),是傅立葉變換在時域和頻域上都呈離散的形式,將信號的時域採樣變換為其DTFT的頻域採樣。在形式上,變換兩端(...
