離散分數傅立葉變換是用來解決數字序列分數傅立葉變換的計算問題,方法是利用它們的特徵函式展開的表達來實現離散算法。
基本介紹
- 中文名:離散分數傅立葉轉換
- 外文名:Discrete fractional Fourier transform
- 套用:信號系統
- 學科:數學
背景
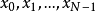
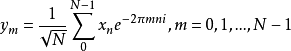
定義
計算方法
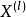
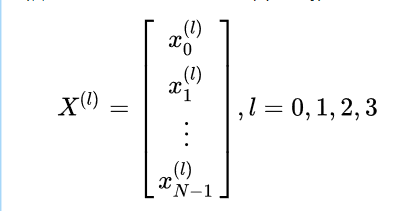 離散傅立葉矩陣形式
離散傅立葉矩陣形式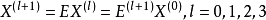
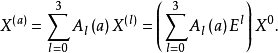
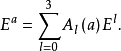
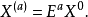
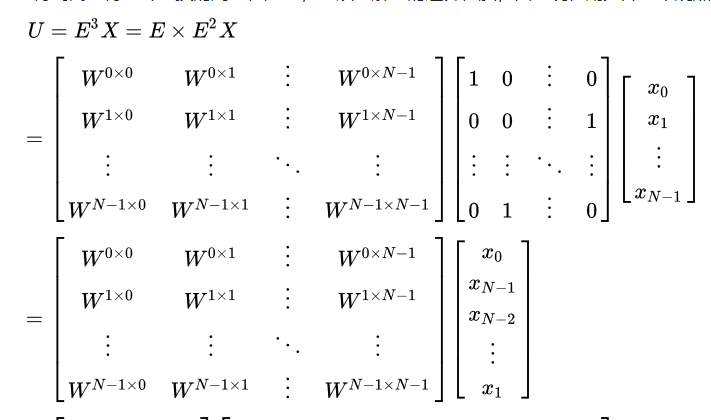
離散分數傅立葉變換是用來解決數字序列分數傅立葉變換的計算問題,方法是利用它們的特徵函式展開的表達來實現離散算法。
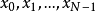
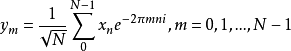
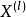
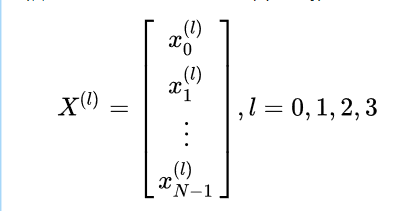 離散傅立葉矩陣形式
離散傅立葉矩陣形式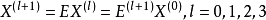
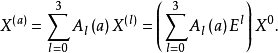
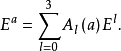
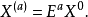
離散分數傅立葉變換是用來解決數字序列分數傅立葉變換的計算問題,方法是利用它們的特徵函式展開的表達來實現離散算法。...
《小波分析與分數傅立葉變換及套用》一書的出版社是國防工業出版社,作者是冉啟文,譚立英。該書可供從事數學研究、圖像處理、信號處理和光學信息處理工作的科研人員、...
由於光學設備很容易實現分數階Fourier變換,所以分數階Fourier變換首先在光信號處理中得到了廣泛的套用。後來分數階Fourier變換的離散化方法的提出,以及其快速計算的實現,...
離散傅立葉變換(Discrete Fourier Transform,DFT)傅立葉分析方法是信號分析的最基本方法,傅立葉變換是傅立葉分析的核心,通過它把信號從時間域變換到頻率域,進而...
離散傅立葉反變換(inverse discrete Fouriertransform)簡稱IDFT一種數字變換的逆變換.頻域有限序列X(k)的離散傅立葉反變換x(n)定義為 ...
快速傅立葉變換 (fast Fourier transform), 即利用計算機計算離散傅立葉變換(DFT)的高效、快速計算方法的統稱,簡稱FFT。快速傅立葉變換是1965年由J.W.庫利和T....
二維離散傅立葉反變換(two-dimensional in-verse discrete Fourier transform)是一種數字變換的逆變換。...
離散傅立葉級數,連續周期信號的連續傅立葉級數有著無窮多的離散頻率分量,相鄰分量的間距由信號的周期決定,等於1/T(角度,弧度乘2π)。...
離散傅立葉擬合法是基於離散傅立葉變換的諧波分析法(有現成的軟體),可對呈周期性波動NDVI時間序列的波動特徵進行分析,並可對高噪聲的NDVI時間序列數據進行降噪。....
用傅立葉變換的方法在頻域中對離散時間線性時不變系統在零狀態下激勵信號產生回響的問題進行分析。...
4.10.1 二維傅立葉變換4.10.2 分數(階)傅立葉變換測試信號處理技術第5章 數字濾波基礎 5.1 線性非移變離散系統時域分析5.1.1 線性非移變離散系統...
4.1分數Fourier變換的定義、性質及快速算法 4.1.1分數Fourier變換的定義 4.1.2分數Fourier變換的性質 4.1.3典型信號的分數Fourier變換 4.1.4離散FrFT及FrFT的快...
