分數階Fourier變換是信號在時頻平面內坐標軸繞原點逆時針旋轉任意角度後構成的分數階Fourier域上的表示方法,是一種廣義的Fourier變換。
基本介紹
- 中文名:分數階傅立葉變換
- 外文名:Fractional Fourier Transform
- 提出時間: 1980年
- 提出者:V.Namias
簡介
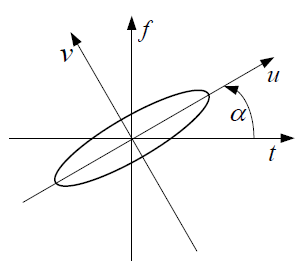 圖1 分數階Fourier變換的時頻變換示意圖
圖1 分數階Fourier變換的時頻變換示意圖分數階Fourier變換是信號在時頻平面內坐標軸繞原點逆時針旋轉任意角度後構成的分數階Fourier域上的表示方法,是一種廣義的Fourier變換。
 圖1 分數階Fourier變換的時頻變換示意圖
圖1 分數階Fourier變換的時頻變換示意圖《分數階傅立葉變換及其套用》是2009年09月清華大學出版社出版的圖書,作者是陶然、王越。本書系統地論述了分數階傅立葉變換的相關研究成果。...
在數學中,連續傅立葉變換是一個特殊的把一組函式映射為另一組函式的線性運算元。 不嚴格地說,傅立葉變換就是把一個函式分解為組成該函式的連續頻率譜。 在數學...
《分數傅立葉光學導論》是2004年科學出版社出版的圖書,作者是冉啟文。...... 經過20多年的發展,分數傅立葉變換這個概念的內涵越來越豐富。分數傅立葉變換作為分數...
2.3.1 序列分數階導數2.3.2 線性分數階微分方程2.3.3 一般的分數階常微分方程2.3.4 例子——Mittag-Leffler函式的套用2.4 附錄A 傅立葉變換...
6.12 分數階傅立葉變換及其套用 參考文獻 習題六 第七章 雷射束在金屬波導中的傳輸 第八章 雷射束在平面介質波導中的傳輸 第九章 光波在光纖中的傳輸詞條...
2. 分數階傅立葉分析及其套用,國家自然科學基金面上項目,2003年12月結題驗收,項目主要組成員。3. 基於分數階傅立葉變換的OFDM系統信道估計及最優階次選擇算法...
第8章 分數階傅立葉變換移動水聲通信技術8.1 大都卜勒頻偏高速移動水聲通信研究背景8.2 分數階傅立葉變換原理及性質8.3 基於frft的水聲信道參數估計...
第2 章研究了基於分數階傅立葉變換的LFM 類信號截獲與特徵提取;第3章研究了基於周期Wigner - Hough 變換的LFMCW 類信號截獲和特徵提取;第4章研究了基於循環譜...
4. 基於分數階傅立葉變換水下目標距離/速度的聯合估計,兵工學報,2011年,vol.32(8): 1030~1035 5. 基於能量UWSAN的最大似然目標定位,西北工業大學學報,2010,...
12.王永學, 陳芳炯, 韋崗. 基於分數階傅立葉變換的正交頻分復用系統同步分析, 電子學報,2006, 34(9): 1690-1693。13.陳芳炯,林耀榮,韋崗. 基於輸出過採樣的...
1. 3. 5分數階傅立葉變換法 121. 3. 6局域波分解法 131. 3. 7自適應陷波器法 141. 4短時信號頻率估計方法 191. 4. 1相干平均法 20...
王強.面向沉底目標的分數階傅立葉變換譜重排回波時頻處理[J], 中南大學學報(自然科學版),2009,40(6):1649-1654. EI。海底鈷結殼採礦車微地形導向聲納探測的...
7.2.3 分數階傅立葉變換法 133 7.3 LFM信號參數的快速高精度估計算法 134 7.3.1 算法介紹 134 7.3.2 收斂條件分析 134 7.3.3 算法仿真與性能...
已在Optics Express 等國內外期刊和會議發表論文30餘篇 [2] ,申報國家發明專利10餘項 [3] ;曾參與專著《分數階Fourier變換的原理與套用》、《分數階傅立葉變換...
市精品課程配套教材·工科數學分析教程(上冊)》將微積分經典內容進行拓展與延伸,力求反映當代數學的發展趨勢,為此引入了分支與混沌、分數階傅立葉變換與小波變換等...
3.2.1基於分數階傅立葉變換的調頻率估計原理041 3.2.2FRFT的算法043 3.2.3時頻中心與尺度因子的初步估計048 3.2.4擬牛頓參數最佳化049 3.2.5參數的進一步...
一種基於極對數分數階傅立葉變換的圖像配準方法 彭靜徐曉艷任蕾(39)基於分形與保局投影的人臉識別算法的研究 李鐵孫勁光劉暘(46)一種基於圖像質量評價的視頻Dissolve...
3.6.2 基於簡化分數階傅立葉變換的運動目標檢測算法3.6.3 仿真結果3.6.4 幾點討論3.7 小結參考文獻第4章 距離向多天線SAR成像4.1 常規距離向多天線SAR的成像...
