運動方程是描述結構中力與位移(包括速度和加速度)關係的數學表達式。其建立方法主要有5種,包括牛頓第二定律、D’Alembert 原理、虛位移原理、Hamilton原理和Lagrange方程。
基本介紹
- 中文名:運動方程
- 外文名:equation of motion
- 定義:描述力與位移(或速度加速度)關係
定義


建立方法
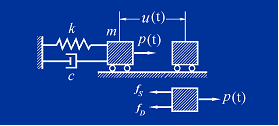
















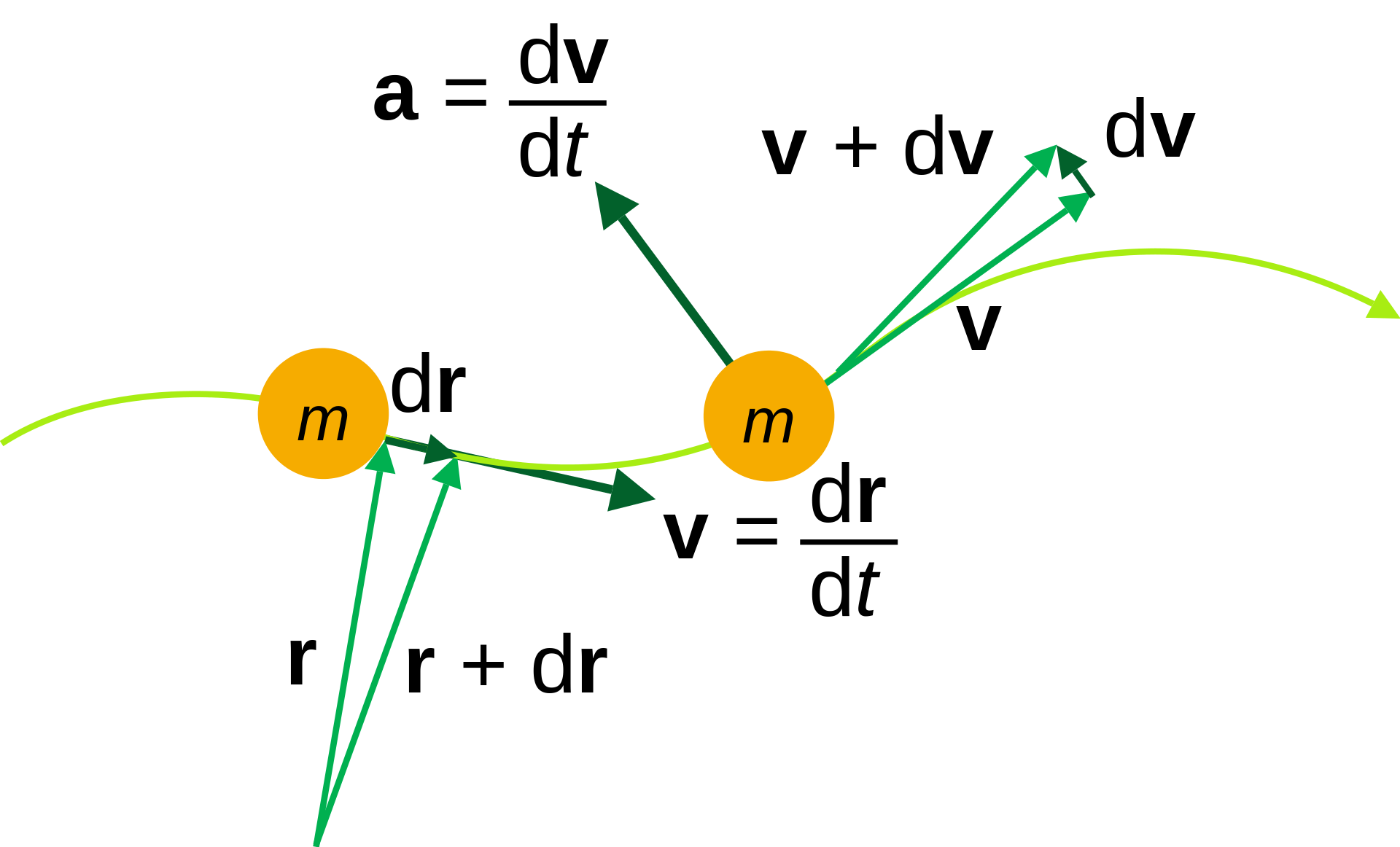
運動方程是描述結構中力與位移(包括速度和加速度)關係的數學表達式。其建立方法主要有5種,包括牛頓第二定律、D’Alembert 原理、虛位移原理、Hamilton原理和Lagrange方程。



















運動方程是描述結構中力與位移(包括速度和加速度)關係的數學表達式。其建立方法主要有5種,包括牛頓第二定律、D’Alembert 原理、虛位移原理、Hamilton原理和Lagrange...
納維-斯托克斯方程(英文名:Navier-Stokes equations),描述粘性不可壓縮流體動量守恆的運動方程。簡稱N-S方程。粘性流體的運動方程首先由Navier在1827年提出,只考慮了...
汽車運動方程(Motor equation)又稱汽車牽引平衡方程。是指汽車在道面上行駛時牽引力與各行駛阻力間的關係式。汽車牽引力又稱汽車驅動力。是指驅使汽車行駛的動力。...
點的運動方程是對點運動過程的數學描述,它能給出任何瞬時t動點所在的空間位置。...... 點的運動方程是對點運動過程的數學描述,它能給出任何瞬時t動點所在的空間位...
活塞運動方程是活塞運動的數學證明形式。活塞頂部在曲軸旋轉中心最遠的位置叫上死點、最近的位置叫下死點、從上死點到下死點的距離叫活塞衝程。活塞式航空發動機大多...
流體運動微分方程是牛頓第二定律的流體力學表達式,是控制流體運動的基本方程,有理想流體運動微分方程和粘性流體運動微分方程。...
《地下水運動方程》是2011年地質出版社出版的圖書,作者是王旭升,萬力。...... 《地下水運動方程》是2011年地質出版社出版的圖書,作者是王旭升,萬力。...
歐拉運動方程Eu1ereqi}atinnofmotionJL稱理想流體運動微分方程。它是1775年著名數學家和力學家歐拉根據理想流體運動時流體所受的力和動量變化推導出的微分方程組。它...
轉子運動方程又稱搖擺方程描述發電機轉子的運動,並將慣性轉矩與轉子上的機械轉矩和電氣轉矩的合成量相關聯,即Jd^2θ/dt^2=Ta (N*m)。式中J是附加在轉子軸上...
運動方程數值解 ...... 圖集 運動方程數值解圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:百科ROBOT...
定義:物體以一定的初速度斜向射出去,在空氣阻力可以忽略的情況下,物體所做的這類運動叫做斜拋運動。物體作勻變速曲線運動,它的運動軌跡是拋物線。...
歐拉運動學方程是描述剛體運動的微分方程,在剛體繞定點運動中,反映角速度和歐拉角關係的方程,該方程在剛體繞定點運動的研究中有重要地位。...
大氣動力方程(dynamic equations of atmospheric motion )描寫大氣運動和狀態變化的方程。在大氣動力學中,根據經典力學的牛頓運動定律,特別是牛頓第二運動定律,推導出...
拉格朗日方程,因約瑟夫·路易斯·拉格朗日而命名,是拉格朗日力學的主要方程,可以用來描述物體的運動,特別適用於理論物理的研究。拉格朗日方程的功能相等於牛頓力學中的牛頓...
簡諧運動(Simple harmonic motion)(SHM)隨時間按餘弦(或正弦)規律的振動,或運動。又稱簡諧振動。簡諧運動是最基本也最簡單的機械振動。當某物體進行簡諧運動時,...
運動方程分析解...... 運動方程分析解 中文名稱 運動方程分析解 英文名稱 analytical solution of motion equation 定義 用分析方法求解的運動方程在給定時刻的位置...
氣體作為一種流體,其運動所遵循的物理規律的數學表達式,用來研究氣體運動中各物理量間的變化關係和求解流場中各物理量的分布。...
波動方程或稱波方程(英語:wave equations) 由麥克斯韋方程組導出的、描述電磁場波動特徵的一組微分方程,是一種重要的偏微分方程,主要描述自然界中的各種的波動現象,...
剛體運動學(kinematics of a rigid body)是研究剛體各種運動的幾何性質的學科。剛體的運動分為平移、定軸轉動、平面運動、定點轉動及一般運動,是分析力學的研究內容...
