活塞運動方程

活塞運動方程是活塞運動的數學證明形式。活塞頂部在曲軸旋轉中心最遠的位置叫上死點、最近的位置叫下死點、從上死點到下死點的距離叫活塞衝程。活塞式航空發動機大多是四衝程發動機，即一個氣缸完成一個工作循環，活塞在氣缸內要經過四個衝程，依次是進氣衝程、壓縮衝程、膨脹衝程和排氣衝程。

基本介紹

• 中文名：活塞運動方程
• 外文名：Piston equation of motion
• 工作原理：活塞頂部在曲軸旋轉中心最遠

曲軸幾何

定義

活塞桿長度（活塞銷與曲柄銷之間的距離）

曲柄半徑（曲柄銷與曲柄中心之間的距離，即半行程）

曲軸轉角（從缸膛中心線開始）

活塞銷位置（從曲軸中心沿缸膛中心線向上）

活塞銷速度（從曲軸中心沿缸膛中心線向上）

活塞銷加速度（從曲軸中心沿缸膛中心線向上）

曲柄角速度

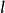
角速度

所述曲軸的角速度，即是發動機每分鐘轉數（RPM）：

三角關係

如圖一所示，曲柄銷，曲柄中心和活塞銷形成角NOP。根據餘弦定理可以看出：

圖一

關於角度位置的方程

以下公式描述活塞相對於曲軸轉角的往復運動。下面顯示了這些方程的示例圖。

位置

相對於曲軸轉角的位置（通過重新排列三角關係）：

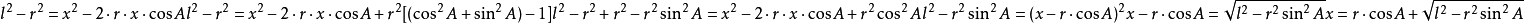
速度

相對於曲軸轉角的速度（採用一階導數，使用鏈式法則）：

加速

關於曲軸轉角的加速度（採用二階導數，使用鏈式法則和商法則）：

時間方程

角速度導數

如果角速度是恆定的，那么

並適用以下關係：

從角度域轉換到時域

下面的等式描述了活塞相對於時間的往復運動。如果時間域是必需的，而不是角度域，先用 ω 取代在等式噸，然後擴展為角速度如下：

位置

單純相對於時間的位置即是：

速度

相對於時間的速度（使用鏈式法則）：

加速

相對於時間的加速度（使用鏈式法則和乘積法則以及角速度導數）：

角速度的比例關係

速度最大值和最小值

加速過零點

速度的最大值和最小值都沒有在曲柄角度發生（A）加或減90°。速度最大值和最小值出現取決於桿長（l）和半行程（r）的曲柄角上，並且對應於加速度為零（橫過水平軸）的曲柄角。

曲柄桿角度不正確

當曲柄與桿成直角時，速度最大值和最小值不一定會發生。有反例證明當曲柄角度正確時速度最大值/最小值出現的觀點。

示例

對於 6 英寸的連桿長和 2 英寸的曲柄半徑，通過數值求解加速度過零點，可確定速度最大值/最小值在曲柄角±73.17615°處。然後使用三角正弦定律，發現曲柄角為88.21738°，桿垂直角為18.60647°。在這個例子中，顯然地曲柄和連桿之間的角度並不是直角。

總結三角形的角度 88.21738°+ 18.60647°+ 73.17615°給出 180.000°。這個反例就反駁了“速度最大值/最小值是發生在當曲柄與桿成直角時”的說法。