基本介紹
- 中文名:特徵值
- 外文名:Eigen value
- 時間:1904
- 提出:希爾伯特
- 分類:數學
- 屬於:線性代數
簡介
定義
基本定義

廣義特徵值

計算方法









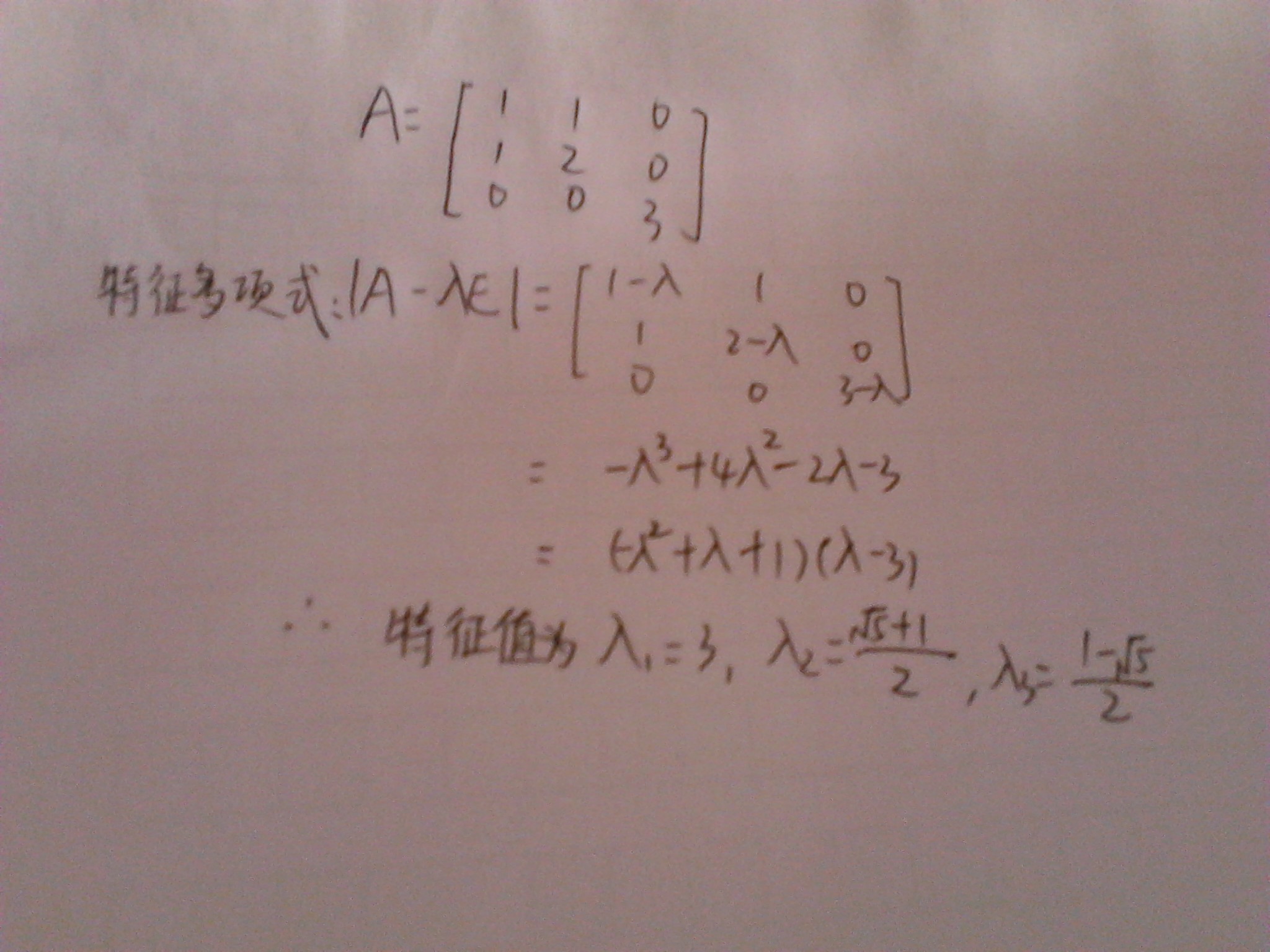











特徵值是線性代數中的一個重要概念。在數學、物理學、化學、計算機等領域有著廣泛的套用。設 A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,...
設A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,則稱 m 是矩陣A的一個特徵值(characteristic value)或本徵值(eigenvalue)。...
概念 一個矩陣可以有多個特徵值,在這些特徵值中,模最大的那個特徵值即主特徵值(對於實數陣即絕對值最大的特徵值),主特徵值對應的特徵向量稱為主特徵向量。 ...
矩陣的特徵向量是矩陣理論上的重要概念之一,它有著廣泛的套用。數學上,線性變換的特徵向量(本徵向量)是一個非簡併的向量,其方向在該變換下不變。該向量在此...
特徵值和特徵向量(eigenvalue and eigenvector)數學概念。若σ是線性空間V的線性變換,σ對V中某非零向量x的作用是伸縮:σ(x)=aζ,則稱x是σ的屬於a的特徵...
特徵值條件數(condition number of eigenva-lue),是衡量特徵值病態程度的標準。...... 特徵值條件數(condition number of eigenva-lue),是衡量特徵值病態程度的標...
特徵分解(Eigendecomposition),又稱譜分解(Spectral decomposition)是將矩陣分解為由其特徵值和特徵向量表示的矩陣之積的方法。需要注意只有對可對角化矩陣才可以施以...
承載力特徵值是在地基設計里,大多採用特徵值,而不是設計值或標準值。實際上,這裡的特徵值,同時具備了設計值和標準值的含義。...
河川徑流特徵的統計值。反映河川徑流量隨時間變化的統計參數。依據自然現象與工程實用要求,河川徑流特徵一般指各年的年平均流量、各月的月平均流量,一年中最大的洪水...
地基承載力特徵值是指由載荷試驗確定的地基土壓力變形曲線線性變形段內規定的變形所對應的壓力值,其最大值為比例界限值。影響地基承載力的主要因素有:地基土的成因...
特徵方程是為研究相應的數學對象而引入的一些等式,它因數學對象不同而不同,包括數列特徵方程、矩陣特徵方程、微分方程特徵方程、積分方程特徵方程等等。...
特徵提取是計算機視覺和圖像處理中的一個概念。它指的是使用計算機提取圖像信息,決定每個圖像的點是否屬於一個圖像特徵。特徵提取的結果是把圖像上的點分為不同的子...
冪法主要用於計算矩陣的按模為最大的特徵值和相應的特徵向量。...... 冪法主要用於計算矩陣的按模為最大的特徵值和相應的特徵向量 [1] 。冪法求矩陣特徵值基本...
對於形式如下的特徵值問題:求數λ,使方程Ax=λBx有非零解x,這裡A為n階實對稱矩陣,B為n階實對稱正定矩陣,x為n維列向量,則稱該問題為矩陣A相對於矩陣B的...
《代數特徵值問題》是2006年科學出版社出版的圖書,作者是J.H.威爾金森。...... 《代數特徵值問題》是2006年科學出版社出版的圖書,作者是J.H.威爾金森。...
介紹 病態特徵值問題(ill-conditioned algebraiceigenvalue problem)一類特殊的特徵值問題.指當矩陣元素的微小擾動引起其某個特徵值(或特徵向量)的巨大變化時的特徵值...
非齊次特徵值通常特徵值問題在實方陣集合里的推廣.實方陣之非齊次特徵值問題在約束特徵值問題、微分方程穩定性問題的研究中有著廣泛的套用。...
剛度特徵值是結構設計中計算的參數,是反映總框架和總剪力牆剛度之比的一個參數,對框架剪力牆結構的受力狀態和變形及外力的分配都有很大的影響。...
水文特徵值:研究水文變化的定量值,用以表示一定時段(日、月、年、多年)內的水文要素的特徵,如最大、最小、平均值等。...
自伴特徵值問題(self-adjoint eigenvalue problem)是在數學物理和運算元理論中占有重要地位的一類帶參數的邊值問題。...
設A是n × n矩陣,λi是其特徵值,i = 1,2,……,n。稱ρ(A)=max{|λi|,i=1,2,……n}為A的譜半徑。即矩陣A的譜半徑等於矩陣A的特徵值的模的最...
在數學中,矩陣或者有界線性運算元的譜半徑是指其特徵值絕對值集合的上確界,一般若為方陣A的譜半徑則寫作ρ(A)。...
