基本介紹
- 中文名:矩陣特徵值
- 外文名:matrix eigenvalues
- 學科:數學
- 領域:線性代數
- 相關概念:特徵向量
- 對象:n階方陣
定義
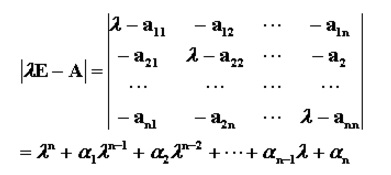


性質
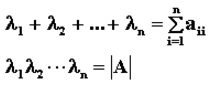
特徵值與特徵向量的求法
方法
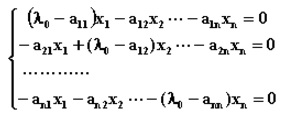
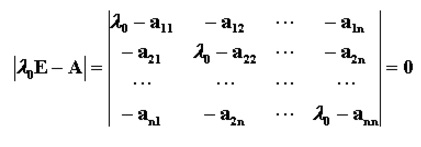
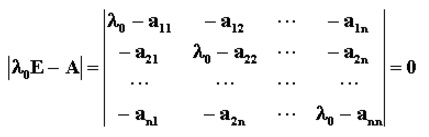
示例

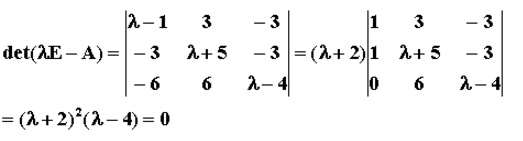
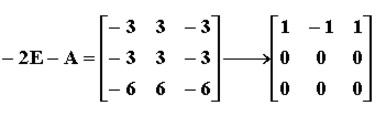
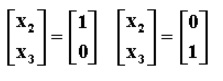
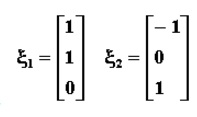
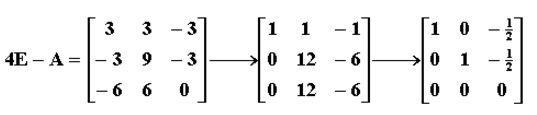
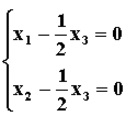
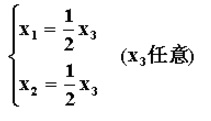


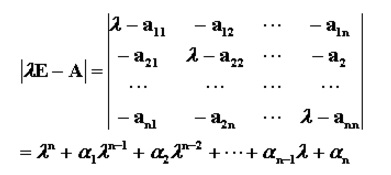


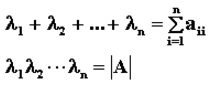
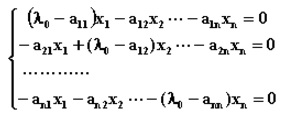
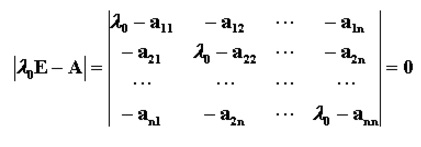
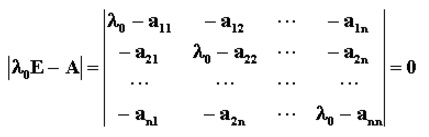

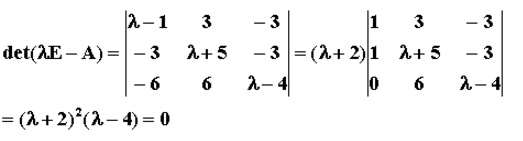

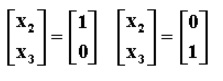


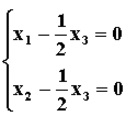
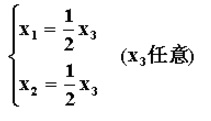

設A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,則稱 m 是矩陣A的一個特徵值(characteristic value)或本徵值(eigenvalue)。...
特徵值是線性代數中的一個重要概念。在數學、物理學、化學、計算機等領域有著廣泛的套用。設 A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,...
冪法主要用於計算矩陣的按模為最大的特徵值和相應的特徵向量。...... 冪法主要用於計算矩陣的按模為最大的特徵值和相應的特徵向量 [1] 。冪法求矩陣特徵值基本...
特徵值和特徵向量(eigenvalue and eigenvector)數學概念。若σ是線性空間V的線性變換,σ對V中某非零向量x的作用是伸縮:σ(x)=aζ,則稱x是σ的屬於a的特徵...
概念 一個矩陣可以有多個特徵值,在這些特徵值中,模最大的那個特徵值即主特徵值(對於實數陣即絕對值最大的特徵值),主特徵值對應的特徵向量稱為主特徵向量。 ...
矩陣的特徵向量是矩陣理論上的重要概念之一,它有著廣泛的套用。數學上,線性變換的特徵向量(本徵向量)是一個非簡併的向量,其方向在該變換下不變。該向量在此...
特徵值條件數(condition number of eigenva-lue),是衡量特徵值病態程度的標準。...... 設久是矩陣A的單特徵值,y和x分別是對應的左、右單位特徵向量,即...
AA'的特徵向量組成U,特徵值組成B'B,A'A的特徵向量組成V,特徵值(與AA'相同)組成BB'。因此,奇異值分解和特徵值問題緊密聯繫。如果A是復矩陣,B中的奇異值仍然...
矩陣特徵值與特徵向量 編輯 主條目:特徵值,特徵向量n×n的方塊矩陣A的一個特徵值和對應特徵向量是滿足 的標量以及非零向量 [13] 。其中v為特徵向量, 為特徵值...
矩陣函式的概念與通常的函式概念類似,不同在於矩陣函式的自變數和因變數都是n階矩陣。矩陣函式一般用冪級數表示。矩陣函式與矩陣值函式是矩陣理論的重要內容,它們在...
單位矩陣的特徵值皆為1,任何向量都是單位矩陣的特徵向量。具有重數。因為特徵值之積等於行列式,所以單位矩陣的行列式為1。因為特徵值之等於跡數,單位矩陣的跡為 ...
特徵方程是為研究相應的數學對象而引入的一些等式,它因數學對象不同而不同,包括數列特徵方程、矩陣特徵方程、微分方程特徵方程、積分方程特徵方程等等。...
分塊矩陣有相應的加法、乘法、數乘、轉置等運算的定義,也可進行初等變換。 分塊矩陣的初等變換是線性代數中重要而基本的運算,它在研究矩陣的行列式、特徵值、秩等...
介紹 病態特徵值問題(ill-conditioned algebraiceigenvalue problem)一類特殊的特徵值問題.指當矩陣元素的微小擾動引起其某個特徵值(或特徵向量)的巨大變化時的特徵值...
也可以將這三種值通過除以 進行標準化。拉普拉斯矩陣示例 編輯 圖度矩陣鄰接矩陣拉普拉斯矩陣 度矩陣 拉普拉斯矩陣性質 編輯 拉普拉斯矩陣是半正定矩陣; 特徵值中0...
(1)n階埃爾米特矩陣A為正定(半正定)矩陣的充要條件是A的所有特徵值大於(大於等於)0。(2)若A是n階埃爾米特矩陣,其特徵值對角陣為V,則存在一個酉矩陣U,使...
直接配置法是按給定的點位誤差橢圓元素構造準則矩陣,或用奇異值分解法來縮減協因數矩陣的特徵值,使所構造的準則矩陣滿足特定的要求.用解析法進行控制網最佳化設計時,...
的矩陣是:旋轉矩陣三維空間 編輯 在三維空間中,旋轉矩陣有一個等於單位1的實特徵值。旋轉矩陣指定關於對應的特徵向量的旋轉(歐拉旋轉定理)。如果旋轉角是 θ,則旋...
包含M矩陣類在內的重要矩陣類,線上性互余及其他許多領域都有廣泛的套用.設A=...xDxAx>0.2.A的每一實特徵值皆正.3.對每一符號差陣S,有x≥0使SASx>0....
顯然,埃爾米特矩陣主對角線上的元素都是實數的,其特徵值也是實數。對於只包含實數元素的矩陣(實矩陣),如果它是對稱陣,即所有元素關於主對角線對稱,那么它也是埃爾...
本原矩陣(primitive matrix)亦稱素矩陣,非負不可約矩陣的重要子類,它同循環陣共同組成了非負不可約矩陣類。介紹若一個n階非負不可約矩陣(A的模=單特徵值的個...
③ 相似矩陣的特徵值相同④相似矩陣的跡相同(=∑λi用在對角矩陣的全部特徵值)2、秩⑤相似矩陣(等價)的秩相同。3、伴隨矩陣集:...
《代數特徵值問題》是2006年科學出版社出版的圖書,作者是J.H.威爾金森。...... 《代數特徵值問題》共分九章。第一章敘述矩陣理論,第二、三章介紹攝動理論和向後...
1、矩陣的譜半徑和範數的關係定義:A是n階方陣,λi是其特徵值,i=1,2,…,n。則稱特徵值的絕對值的最大值為A的譜半徑,記為ρ(A)。 注意要將譜半徑與譜...
(8)P,Q為可逆矩陣, 則 r(PA)=r(A)=r(AQ)=r(PAQ) [4] (9)若矩陣可相似對角化則矩陣的秩等於矩陣非零特徵值的個數。...
