拉普拉斯矩陣

拉普拉斯矩陣(Laplacian matrix) 也叫做導納矩陣、基爾霍夫矩陣或離散拉普拉斯運算元，主要套用在圖論中，作為一個圖的矩陣表示。

基本介紹

• 中文名：拉普拉斯矩陣
• 外文名：Laplacian matrix
• 別稱：導納矩陣，吉爾霍夫矩陣
• 主要套用：在圖論中，作為一個圖的矩陣表示

定義

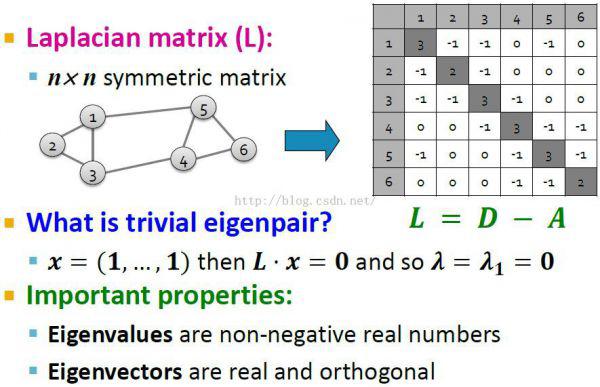
給定一個有n個頂點的圖G，它的拉普拉斯矩陣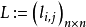 定義為:

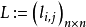
L=D-A

其中D為圖的度矩陣，A為圖的鄰接矩陣。度矩陣在有向圖中，只需要考慮出度或者入度中的一個。經過計算可以得

1、若i =j,則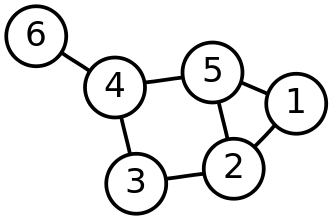

為頂點 的度。

2、若i≠ j,但頂點 和頂點 相鄰，則

3、其它情況

也可以將這三種值通過除以 進行標準化。

示例

圖	度矩陣	鄰接矩陣	拉普拉斯矩陣
	度矩陣

性質

1. 拉普拉斯矩陣是半正定矩陣；
2. 特徵值中0齣現的次數就是圖連通區域的個數；
3. 最小特徵值是0，因為拉普拉斯矩陣每一行的和均為0；
4. 最小非零特徵值是圖的代數連通度。