基本介紹
- 中文名:矩陣的跡
- 外文名:trace
- 學科:數學、線性代數
- 簡稱:tr(X)
矩陣的跡,性質,
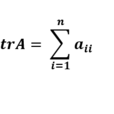
線上性代數中,一個n×n矩陣A的主對角線(從左上方至右下方的對角線)上各個元素的總和被稱為矩陣A的跡(或跡數),一般記作tr(A)。...
跡,是線性代數中的概念,矩陣的跡:主對角線(左上至右下的那一條)上所有元素之和。記作tr(A),其中A為方陣。...
跡數,又稱跡,矩陣的跡。一個矩陣的跡是其特徵值的總和(按代數重數計算)。跡的英文為trace,是來自德文中的Spur這個單字(與英文中的Spoor是同源詞),在數學中,...
在數學中,跡類運算元(英語:Trace class)是一個滿足如下條件的緊運算元,可以為其定義跡,使得跡有限且與基底的選擇無關。跡類運算元本質上與核型運算元相同,但是許多作者...
矩陣單位,即單位矩陣。線上性代數中,n階單位矩陣,是一個n*n的方形矩陣,其主對角線元素為1,其餘元素為0。...
設tr(·)是ℳ+上的跡,若當{Aα}為ℳ+的向上有向族,且 A 為此族的上確界時,總有tr(A)=sup tr(Aα),則稱 tr 為正規跡。...
tr(A)=the trace of the matrix A 矩陣A的跡。...... (數學概念符號(矩陣))編輯 鎖定 tr(A)=the trace of the matrix A 矩陣A的跡。...
相似不變數(similarity invariant)一般指相似變換的一種特徵,即圖形經過任何相似變換都不改變的量,例如,相似比就是最基本的相似不變數。相似不變數也指相似矩陣的...
第十講 矩陣的跡習題十第十一講 線性空間與線性變換11.1 線性空間11.1.1 基本概念與主要定理11.1.2 典型例題解析11.2 線性變換11.2.1 基本概念與重要定理...
