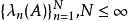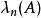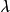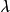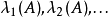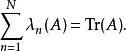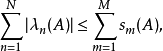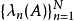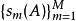跡類運算元

在數學中，跡類運算元（英語：Trace class）是一個滿足如下條件的緊運算元，可以為其定義跡，使得跡有限且與基底的選擇無關。跡類運算元本質上與核型運算元相同，但是許多作者將希爾伯特空間上的核型運算元這一特殊情況稱為“跡類運算元”，而將“核型運算元”用於更一般的巴拿赫空間。

基本介紹

• 中文名：跡類運算元
• 外文名：Trace class
• 領域：數學

定義

模擬矩陣的定義，在可分希爾伯特空間H上的有界線性運算元A被稱為屬於跡類，如果對於H的所有標準正交基{e_k}_k

有限。此時

絕對收斂且不依賴於標準正交基的選擇。這個值被稱為A的跡。當H是有限維空間時，每個線性運算元都是跡類的，並且A的跡的定義與矩陣的跡的定義一致。

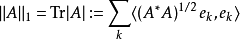
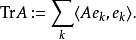
如果A是非負自伴運算元，我們也可以通過可能發散的求和將A的跡定義為擴展實數

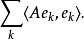
性質

概述

如果A是非負自伴運算元，若且唯若Tr(A)<∞時，A是跡類的。 因此，自伴運算元A是跡類的，若且唯若其正部A和負部A都是跡類的。 （自伴運算元的正負部通過連續泛函演算得到。）

跡是跡類運算元空間上的線性泛函，即

雙射

是跡類運算元空間上的內積；相應的範數被稱為希爾伯特-施密特範數。 跡類運算元在希爾伯特-施密特範數意義下的完備化被稱為希爾伯特-施密特運算元。

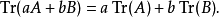
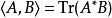
如果A有界且B是跡類的，則AB和BA也是跡類的，且有

此外，在同樣的假設下

最後的斷言在A和B都是希爾伯特-施密特運算元這樣較弱的假設下也成立。

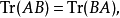
如果A是跡類的，則可以定義1+A的弗雷德霍姆行列式

其中 是A的譜。A的跡類條件保證這一無限乘積是有限的：實際上

這還意味著 若且唯若 是可逆的。

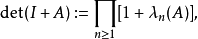
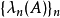
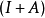
Lidskii定理

令A是可分希爾伯特空間H中的跡類運算元，並且令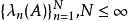為A的特徵值。 假設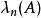在計數時考慮了代數重數（即如果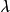的代數重數為k，則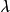在計數時被重複K次如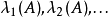）。Lidskii定理（以Victor Borisovich Lidskii命名）指出

注意到由於外爾不等式，左側的數列絕對收斂

在特徵值和緊運算元A的奇異值之間。