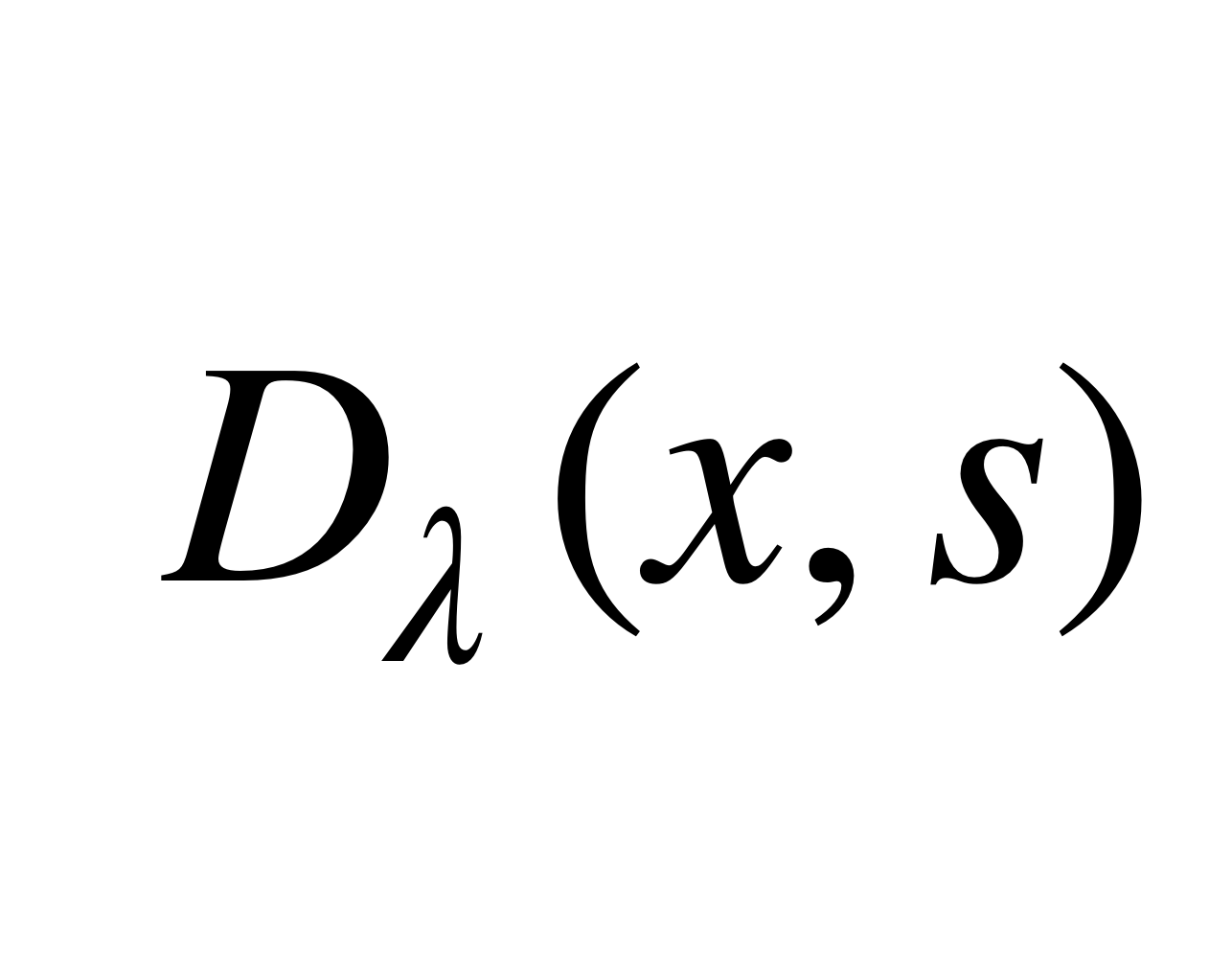弗雷德霍姆行列式(Fredholm determinant)是一個由弗雷德霍姆線性積分運算元的核確定的行列式。
基本介紹
- 中文名:弗雷德霍姆行列式
- 外文名:Fredholm determinant
- 適用範圍:數理科學
簡介,弗雷德霍姆積分方程,
簡介
對於弗雷德霍姆積分方程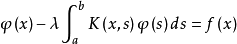 ,弗雷德霍姆於1900年在假定區間[a,b]有限,核K(x,s)與自由項f(x)為連續的條件下,使方程的求解問題得以完全解決。他的思想是把積分方程與代數方程組做類比,直接利用行列式求解,並把方程的解表示為兩式的商。這一方法與求解線性方程組的克萊姆法則類似。具體來說,就是用離散方程
,弗雷德霍姆於1900年在假定區間[a,b]有限,核K(x,s)與自由項f(x)為連續的條件下,使方程的求解問題得以完全解決。他的思想是把積分方程與代數方程組做類比,直接利用行列式求解,並把方程的解表示為兩式的商。這一方法與求解線性方程組的克萊姆法則類似。具體來說,就是用離散方程 逼近原積分方程,並分別取
逼近原積分方程,並分別取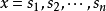 ,則得到未知量為
,則得到未知量為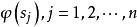 的線性方程組
的線性方程組 。
。
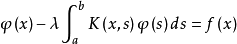

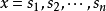
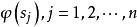

若λ不是方程組係數行列的特徵根,可求出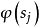 得積分方程近似解
得積分方程近似解
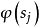


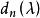


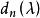


弗雷德霍姆積分方程
形如