弗雷德霍姆理論是關於線性積分運算元的基本理論之一,是弗雷德霍姆(Fredholm,E.I.)通過積分方程與線性代數方程組類比的方法(即把線性積分方程看成是“無窮維”線性方程組)於1900年獲得的。
基本介紹
- 中文名:弗雷德霍姆理論
- 外文名:Fredholm theory
- 適用範圍:數理科學
簡介
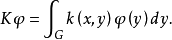
弗雷德霍姆第一定理
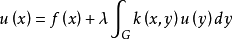
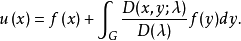
弗雷德霍姆第二定理
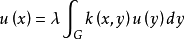
弗雷德霍姆第三定理

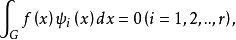
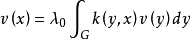
弗雷德霍姆理論是關於線性積分運算元的基本理論之一,是弗雷德霍姆(Fredholm,E.I.)通過積分方程與線性代數方程組類比的方法(即把線性積分方程看成是“無窮維”線性方程組)於1900年獲得的。
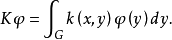
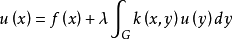
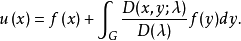
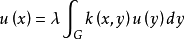

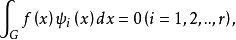
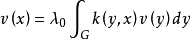
弗雷德霍姆理論是關於線性積分運算元的基本理論之一,是弗雷德霍姆(Fredholm,E.I.)通過積分方程與線性代數方程組類比的方法(即把線性積分方程看成是“無窮維”線性方程...
弗雷德霍姆定理(Fredholm theorems)積分方程的基本定理.設第二類弗雷德霍姆積分方程是稱為方程(1)的轉置方程。...
弗雷德霍姆(1866~1927),瑞典數學家。積分方程理論的創始人之一。...... 弗雷德霍姆(1866~1927),瑞典數學家。積分方程理論的創始人之一。中文名 弗雷德霍姆 外文...
弗雷德霍姆線性積分運算元是一類重要的線性積分運算元,是n維空間上的線性運算元當n變成無窮時的極限式。...
里斯-紹德爾理論就是關於巴拿赫空間上的全連續運算元與20世紀初對第二類積分方程所建立的弗雷德霍姆定理相對應的理論。...
1.1.2 第二類弗雷德霍姆(Fr)積分方程1.1.3 積分方程與微分方程之間的關係1.2 長球面波函式的微分方程1.3 長球面波函式微分方程與積分方程理論上的統一...
20世紀初,在討論第二類線性積分方程時,也得到了和線性方程組完全類似的弗雷德霍姆理論。後來,人們發現這種理論對(線性)全連續運算元也是成立的。...
里斯、J.P.紹德爾建立了巴拿赫全連續運算元的弗雷德霍姆理論。1904~1906年D.希爾伯特考察了具有對稱核的積分方程,後來又有了一般的有界自共軛運算元的譜理論。20年代J...
至於第一種弗雷德霍姆積分方程,早在1828年就為G.格林在研究位勢理論以解決拉普拉斯方程的狄利克雷問題時所導出。線性積分方程理論的發展,始終與數學物理問題的研究...
弗雷德霍姆積分方程的重要推廣和發展,包括允許積分核有不可積的奇點,積分區間是無限區間等多種情形。使弗雷德霍姆定理不成立的線性積分方程,通常稱為奇異積分方程。...
柯西奇異積分方程(Cauehy singular integral equations)是一類最基本且具有廣泛實際套用的奇異積分方程,其積分是柯西主值意義下的。柯西奇異積分方程與弗雷德霍姆積分...
他在積分方程中引進復參數方法,促進了弗雷德霍姆理論的發展。龐加萊對現代數學最重要的影響是創立組合拓撲學。1892年他發表了第一篇論文,1895~1904年,他在六篇...
積分方程論中許多思想和方法,例如,關於第二種弗雷德霍姆(Fredholm)積分方程的弗雷德霍姆理論和奇異積分方程的諾特(Noether)理論以及逐次逼近方法,本身就是數學中經典而...
出現在方程中的積分運算元是有界運算元甚至是有逆的,而後者只是相應函式空間中的緊運算元,緊運算元除有限維運算元外是沒有有界逆的,這就是弗雷德霍姆理論不能套用到奇異...
他在積分方程中引進復參數方法,促進了弗雷德霍姆理論的發展。龐加萊對現代數學最重要的影響是創立組合拓撲學。1892年他發表勒第一篇論文,1895~1904年,他在六篇...
