設X、Y均為距離空間,T為X→Y的線性運算元,如果T將X中的任一有界集映成Y中的列緊集,則T稱為緊運算元,連續的緊運算元稱作全連續運算元。如果X、Y均為賦范線性空間,則T是緊運算元與T是全連續運算元是等價的。
基本介紹
- 中文名:全連續運算元
- 外文名:Completely continuous operator
- 概述:連續的緊運算元
- 特點:最接近於有限維空間上線性運算元
- 領域:泛函分析
- 學科:數學
簡介
定義
性質
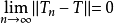
設X、Y均為距離空間,T為X→Y的線性運算元,如果T將X中的任一有界集映成Y中的列緊集,則T稱為緊運算元,連續的緊運算元稱作全連續運算元。如果X、Y均為賦范線性空間,則T是緊運算元與T是全連續運算元是等價的。
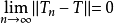
設X、Y均為距離空間,T為X→Y的線性運算元,如果T將X中的任一有界集映成Y中的列緊集,則T稱為緊運算元,連續的緊運算元稱作全連續運算元。如果X、Y均為賦范線性空間...
全連續映射是映有界集為相對緊集的連續映射,緊連續映射必為全連續映射。...... 可微的全連續映射在每點的導運算元是全連續線性運算元。設D為X中的有界閉集,f:D...
線性積分運算元全連續性(complete continu-ity of linear integral operator)全連續性是線性積分運算元特有的基本性質.設k<x,婦是GXG上的平方可積函式,則以k(二,y)...
全連續性是非線性積分運算元的重要性質。如果k(x,y,u)在G×G×R1上連續,則烏雷松非線性積分運算元 是作用在C(G)上的全連續運算元。...
線性積分運算元分解是運算元的一種分解。所謂線性積分運算元的分解,是指把一個線性積分...(G)全連續,這裡1...
希爾伯特空間上的線性全連續運算元源於積分方程論的需要。因此,研究全連續運算元A的特徵值和奇異值(即A*A的特徵值的平方根)就是重要的工作。設 A,B是兩個希爾伯特...
→X是全連續運算元,且0∉(I-A)(∂Ω),故勒雷-紹德爾度deg(I- A,Ω,0)存在,它就定義為F在Ω上關於L的疊合度,記為DL(F,Ω)。疊...
弗雷德霍姆理論是關於線性積分運算元的基本理論之一。設G是RN中具有非零測度的可測集,k(x,y):G×G→R1連續,D(λ)是k(x,y)的弗雷德霍姆行列式,D(x,y;λ)...
7.5.2 全連續運算元習題參考文獻第8章 積分方程8.1 積分方程的基礎理論8.1.1 積分方程的定義和分類8.1.2 積分方程與微分方程的關係...
重點介紹了有界線性運算元和泛函的基本知識; 第 4 章介紹 Banach 空間理論的基本定理, 重點介紹了Hahn-Banach 定理和共鳴定理, 以及弱收斂和全連續運算元的基本概念及...
例如,把積分方程(3)中出現的函式看作是巴拿赫空間X的元素,原來的積分運算以運算元T代替,於是方程(3)就可寫為公式 (8)這裡T是巴拿赫空間X中的一個全連續運算元,ψ...
1.4 全連續運算元譜逼近 1.4.1 Banach空間全連續運算元譜逼近 1.4.2 Hilbert空間自共軛全連續運算元譜逼近 第二章 有限元法數學理論基礎知識 ?2.1 Sobolev空間與...
③(λI-T)有有界逆運算元,但不定義於全空間,稱這種λ為T的剩餘譜,其全體記為σr(T)。④(λI-T)有稠定逆運算元,而逆運算元是無界的,稱這種λ為T的連續譜,...
《集值分析與經濟套用》內容包括空間理論基礎,運算元理論基礎,凸分析基礎,集值映射的連續性,集值映射的凸分析,集值映射的不動點理論,集值映射的拓撲度理論和集值...
