列緊集是度量空間中的一類子集,設A是度量空間X中的無窮集,如果A中的任一無窮子集必有一個收斂的點列,就稱A是X中的列緊集;如果X本身是列緊集,就稱X是列緊距離空間,簡稱為列緊空間。列緊集是有界的。需要注意的是,一般度量空間與歐氏空間不同,有界閉集一定列緊。
基本介紹
- 中文名:列緊集
- 外文名:sequentially compact set
- 性質1:列緊集是有界的
- 性質2:任意空間的所有有限點集是列緊的
- 必要條件:該集合為完全有界的
- 套用學科:泛函分析
預備知識

定義
性質
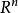
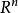
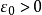
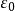
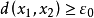
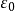
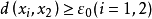
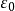
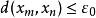
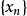
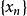
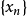
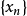
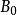
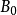
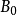
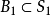
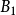
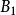
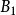
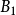
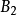
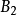
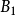
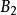
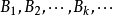
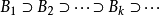
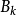
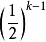
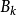
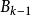
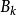
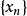

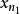
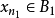
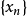
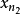
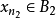
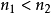
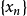
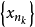
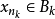
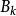

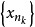

列緊集是度量空間中的一類子集,設A是度量空間X中的無窮集,如果A中的任一無窮子集必有一個收斂的點列,就稱A是X中的列緊集;如果X本身是列緊集,就稱X是列緊距離空間,簡稱為列緊空間。列緊集是有界的。需要注意的是,一般度量空間與歐氏空間不同,有界閉集一定列緊。

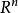
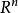
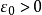
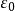
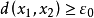
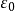
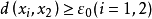
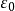
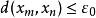
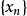
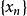
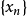
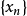
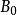
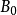
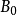
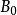
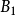
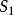
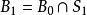
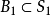
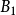
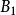
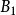
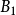
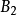
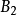
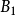
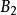
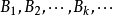
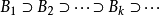
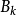
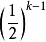
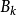
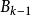
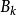
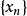

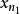
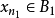
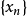
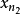
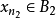
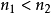
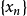
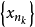
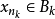
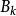

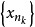
列緊集是度量空間中的一類子集,設A是度量空間X中的無窮集,如果A中的任一無窮子集必有一個收斂的點列,就稱A是X中的列緊集;如果X本身是列緊集,就稱X是列...
完全有界集是指距離空間中的一類子集。度量空間中的列緊集一定是完全有界的,而在完備度量空間中,完全有界性與列緊性等價。...
設X、Y均為距離空間,T為X→Y的線性運算元,如果T將X中的任一有界集映成Y中的列緊集,則T稱為緊運算元,連續的緊運算元稱作全連續運算元。如果X、Y均為賦范線性空間...
柯爾莫哥洛夫定理是關於Lp[a,b]的子集為列緊集的特徵的定理。...... 柯爾莫哥洛夫定理是關於Lp[a,b]的子集為列緊集的特徵的定理。 [1] ...
23.存在某個度量空間中的列緊集,它與它的某個真子集等距 24.存在某個非緊度量空間,它不能與它的真子集等距 25.存在非緊的度量空間,在它上面的每個實值...
1.3.4 緊空間的乘積空間 1.3.5 StoneˉWeierstrass 定理 1.3.6 距離空間中的列緊集與完全有界集 1.3.7 有限維賦范線性空間的特徵 1.3.8 BanachˉAlao...
集和點集、開集、閉集與完全集、測度、可測函式與積分、度量空間、線性運算元與...3 列緊集(緻密集) 4 線性賦范空間 5 凸集與不動點 6 內積空間 第五章 ...
稱拓撲空間X的子集K為緊集, 若能從X的任一覆蓋K的開集族中取有限覆蓋 【相關概念】 1. 列緊:稱X列緊,若X中的任一序列有收斂子列 2...
