設{fn}為定義在實數集E上一列實數值函式,稱{fn}在E上是等度連續的,如果任意ε>o,存在δ>o,使得當|x-y|<δ,x,y∈E及n≥1時,都有|fn(x)-fn(y)|<ε。顯然,如果{fn}在E上等度連續,則對每一個n,函式fn(x)在E上一致連續。
基本介紹
- 中文名:等度連續
- 外文名:equicontinuous
- 所屬學科:數學
- 相關定理:Ascoli-Arzela定理
- 相關概念:緊緻集、點式有界、一致有界等
定義
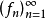
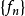
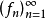
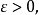
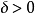
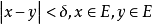
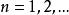
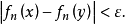
相關命題
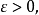
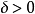
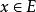
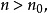
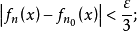
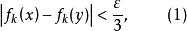
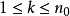
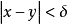
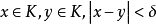
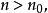
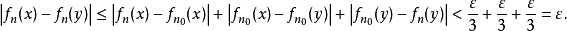
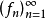
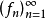
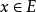
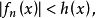
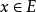
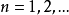
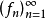
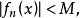
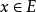
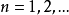
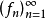
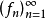
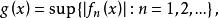
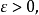
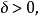
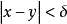
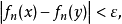
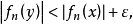
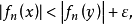

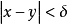
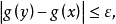
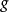
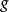
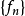
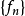
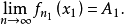
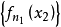
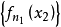
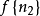
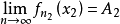
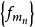
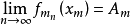
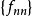
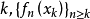
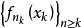
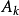
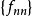
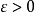
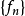
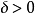
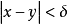
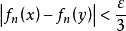
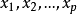
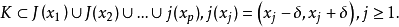
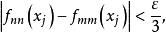
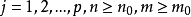
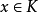
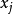
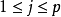
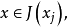
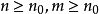
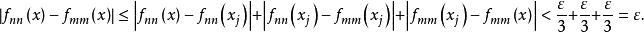
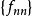

設{fn}為定義在實數集E上一列實數值函式,稱{fn}在E上是等度連續的,如果任意ε>o,存在δ>o,使得當|x-y|<δ,x,y∈E及n≥1時,都有|fn(x)-fn(y)|<ε。顯然,如果{fn}在E上等度連續,則對每一個n,函式fn(x)在E上一致連續。
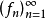
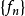
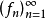
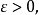
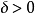
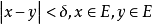
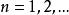
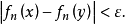
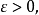
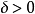
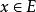
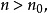
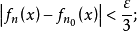
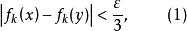
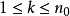
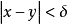
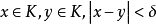
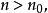
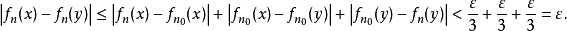
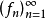
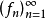
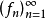
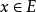
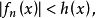
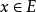
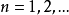
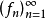
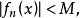
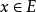
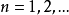
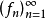
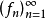
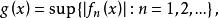
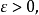
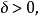
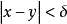
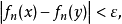
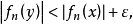
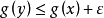
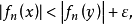

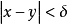
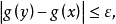
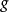
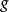
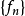
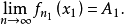
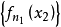
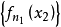
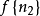
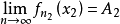
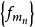
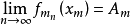
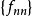
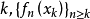
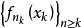
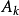
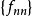
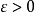
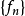
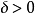
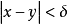
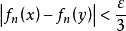
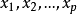
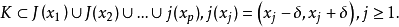
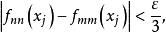
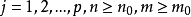
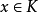
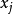
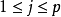
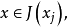
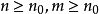
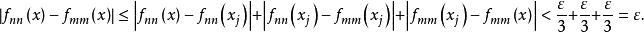
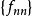
設{fn}為定義在實數集E上一列實數值函式,稱{fn}在E上是等度連續的,如果任意ε>o,存在δ>o,使得當|x-y|<δ,x,y∈E及n≥1時,都有|fn(x)-fn(y)...
函式族是數學中最重要的概念之一。它是從大量實際問題中抽象出來的,體現出合乎形式邏輯和辯證邏輯的數學思維。等度連續函式族(family of equicontinuousfunctions)...
集值等度連續族(set-valued equicontinuousfamily)一類特殊的集值映射族.設X為拓撲空間,(Y,`}l)為一致空間,M(X ,Y)為X到Y的集值映射全體,}CM(X,Y),...
C0類等度連續運算元半群是具有等度連續性的C0類運算元半群,是巴拿赫空間上C0類運算元半群的直接推廣。...
(V>CU,則稱鄉獷是齊連續函式族.設厭是拓撲空間X到一致空間(Y ; }l)的映射族.若了是等度連續的,則.是齊連續的.反之,若了是齊連續的,並且對於任意二EX...
那么C(X)的緊緻開拓撲上的一個子集F具有一致範數的充要條件是它是等度連續駐點有界的。註記C(X)是X上的所有實連續函式所組成的空間....
則稱F在x是等度連續的。若F在X的每點都是等度連續的,則稱F是等度連續函式族。若F是等度連續函式族,則F上的點態收斂拓撲是聯合連續的。若F關於聯合連續...
中每個等度連續集合 上, 和 是一致的。⇒ :按 定理,每個等度連續集合 關於 拓撲是相對緊的,從而關於 也是相對緊的。⇒ :局部凸空間 中的每個有界集 ,由...
設{Tt|t≥0}是序列完備的局部凸拓撲線性空間X上的C0類等度連續運算元半群,則共軛空間X*上的{Tt*|t≥0}滿足半群性質,關於t≥0等度連續,但一般不是C0類的...
其中,函式的連續性、可微性認為是局部性質,而凸性、單調性、稠密性、等度連續性、李普希茲連續、水平集等通常稱為全局性的解析性質。...
A.復坐標下的連續函式B.連續函式序列C.等度連續習題1.4 平面曲線A.曲線的表示B.連續集C.連續的輻角函式習題第2章 可微函式52.1 函式的微分...
X是列緊空間,F⊂C(X)是列緊的充要條件是F是一致有界並且等度連續的。 [2] 參考資料 1. 羅躍生 杜維華主編.泛函分析.哈爾濱:哈爾濱工程大學出版社,2007:...
4.如所周知,70多年來,建立在等度連續定理、開映射定理、閉圖象定理這三大基本原理基礎上的線性泛函分析理論,取得了巨大成功。然而,這三大基本原理只適用於線性運算元...
《一元微積分基礎理論深化與比較》共10章,主要內容包括實數基本定理與距離結構,實數基本定理與序結構,函式的半連續性、一致連續性與等度連續性,單調函式及其線性...
4.6 等度連續性 4.7 完備性 4.8 巴拿赫代數初探 4.9 壓縮映射不動點定理 4.10 參數弧的積分 4.11 複數系 4.12 弱方法 第五章 內積空間 5.1 內...
一致收斂性與連續性一致收斂性與積分一致收斂性與微分等度連續的函式族Stone-Weierstrass 定理習題第8章 一些特殊函式冪級數指數函式與對數函式...
《拓撲動力系統概論》共有拓撲動力系統基礎、遍歷論基礎、等度連續性與Ellis半群理論、族與弱不交、熵、熵與局部化、序列熵與局部化、傳遞系統的分類、不交性...
設{Tt|t∈(-∞,+∞)}是局部凸拓撲線性空間X上的運算元群,如果{Tt|t≥0}和{St=T-t|t≥0}都是C0類等度連續運算元半群,則稱{Tt|t∈(-∞,+∞)}為C0...
在連續函式空間C([a,b])中,根據Azela-Ascoli定理 [1] ,一個子集是預緊的若且唯若其有界且等度連續。 在完備的度量空間中,一個集合預緊若且唯若任何一...
他和阿斯科利(Ascoli,G. ,1843-1896)共同研究了連續函式族的緊緻性條件,建立了“等度連續且一致有界的函式族的任意序列中必可選出緊一致收斂的子序列”的定理...
把{Tt|t≥0(或t>0)}視定義在[0,+∞)(或(0,+∞))上運算元值函式時,還要假設有某種連續性,具體可見C0類運算元半群,C0類等度連續運算元半群,解析運算元半群等...
把{Tt|t≥0(或t>0)}視定義在[0,+∞)(或(0,+∞))上運算元值函式時,還要假設有某種連續性,具體可見C0類運算元半群,C0類等度連續運算元半群,解析運算元半群等...
2.7等度連續性、遠距性與鄰近性 2.8拓撲回復在Ramsey理論中的套用 第3章符號動力學 3.1子移位與編碼 3.2有限型子移位 3.3 Perron—Frobenius定理 3....
5.7 等度連續性練習五第六章 廣義積分6.1 無限區間上的積分6.2 收斂性判別準則6.3 瑕積分6.4 廣義積分與級數6.5 有限區間上含參量積分...
全書共有拓撲動力系統基礎、遍歷論基礎、等度連續性與Ellis半群理論、族與弱不交、熵、熵與局部化、序列熵與局部化、傳遞系統的分類、不交性以及混沌等10章內容...
此外,對現行教材中比較薄弱的部分,如半連續、凸函式、不等式、等度連續等內容,作了適當擴充。全書共分7章、33節、220個條目、1200個問題,包括一元函式極限、...
