基本介紹
- 中文名:緊緻集
- 外文名:compact set
- 別名:緊集
- 概述:任意開覆蓋包含有限開覆蓋
- 本質:拓撲空間中的集合
- 相關概念:列緊
- 學科:數學
定義
開覆蓋
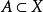
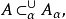
緊緻集(緊集)
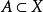
局部緊
性質

證明緊集的方法
常用結論及拓展
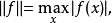
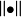

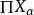
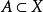
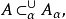
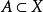

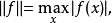
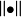

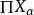
緊緻集是拓撲空間的一類重要子集,亦稱緊緻集。稱A為緊集,若A的任意開覆蓋包含A的有限開覆蓋。有限維賦范線性空間中的有界閉集是緊集。...
緊集是指拓撲空間內的一類特殊點集,它們的任何開覆蓋都有有限子覆蓋。從某種意義上,緊集類似於閉集。...
緊緻,第一層意思是拓撲學中的基本概念,第二層意思是形容很緊,【肉】細膩。...... 直線不是緊緻的,圓圈是緊緻的。 球面和射影直線是緊緻的。凡是有界閉集都是...
緊緻性定理是符號邏輯和模型論中的基本事實,它斷言一階句子的(可能無限的)集合是可滿足的(就是說有一個模型),若且唯若它的所有有限子集是可滿足的。命題演算...
在數學領域的序理論中,偏序集合的緊緻或有限元素是還未包含在緊緻元素之上的成員的任何非空有向子集的上確界所不能包容的那些元素。注意在數學中還有其他的緊緻...
身體緊緻霜是一款護膚品,鐵樹葉子及木頭(採用有強效的抗老功能,可幫助膠原蛋白的合成。能強力消滅自由基,及中和會破壞膠原及彈力纖維的分解酵素。)...
完全有界集是指距離空間中的一類子集。度量空間中的列緊集一定是完全有界的,而在完備度量空間中,完全有界性與列緊性等價。...
設X是局部緊的豪斯多夫空間,𝒰是X上的超調和簇,U是開集。若對f∈𝒰(U),存在緊集K使得在U\K上f≥0,並且∀ξ∈∂U,當x→ξ時lim inf f(x)≥...
完全映射(perfect mapping)亦稱完備映射,一類重要的映射。設X,Y為拓撲空間,映射f:X→Y。若對於任意y∈Y,f(y)是X的緊集,則稱f為緊映射。若f是緊的、閉的...
2.序結構:由集合及其上的序關係組成,如偏序集、全序集、良序集。3.拓撲結構:由集合及其上的拓撲組成,如拓撲空間、度量空間、緊緻集、列緊空間等。...
所有次梯度的集合稱為次微分,記為 。次微分總是非空的凸緊集。次微分歐幾里得空間 歐幾里得幾何是在約公元前300年,由古希臘數學家歐幾里得建立的角和空間中距離...
一般拓撲學亦被稱為點集拓撲學,被用於其他數學領域(如緊緻性與連通性等主題)之中。 代數拓撲學運用同調與同倫群等代數結構量測連通性的程度。 微分拓撲學研究在...
的一個開集 ,令所有集合 構成 的拓撲的一個子基,這個拓撲稱為點態收斂拓撲(...的一個拓撲基,我們稱這個拓撲為緊緻收斂拓撲(topology ofcompact convergence)(有...
§ 1.3 緊性1.3.1 緊集的概念1.3.2 緊集上的連續映射1.3.3 Zorn 引理1.3.4 緊空間的乘積空間1.3.5 StoneˉWeierstrass 定理...
中的閉集;f為凸函式若且唯若 為凸集,根據函式與它的上圖之間的一一對應關係...,且存在一個緊緻集合D,使得對每一i, 非空,則必有 。約束最最佳化問題的逼近理論...
緊凸集是一類重要的凸集,它既是凸集又是緊緻集。...... 緊凸集是一類重要的凸集,它既是凸集又是緊緻集。緊凸集(compact convex set)設X是任一拓撲空間,A是X的...
緊性為點集拓撲中的基本概念,若X的任一開覆蓋有有限子覆蓋,稱拓撲空間X的子集K為緊集,若能從X的任一覆蓋K的開集族中取有限覆蓋。...
預緊(precompact)是數學中的一個基本概念,主要出現在分析學中。一個集合稱為預緊,則該集合的閉包為緊集。...
