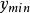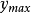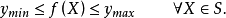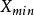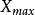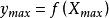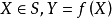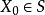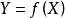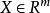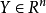緊集是指拓撲空間內的一類特殊點集,它們的任何開覆蓋都有有限子覆蓋。從某種意義上,緊集類似於閉集。
基本介紹
- 中文名:緊集
- 外文名:Compact set
- 所屬學科:數學
- 內涵:特殊點集
- 相關概念:有界、閉集、收斂的子序列等
定義,相關概念,相關性質定理,定理1,定理2,定理3,定理4,
定義
如果一個集合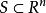 包含在某個球內,也即存在
包含在某個球內,也即存在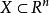 和
和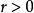 使得
使得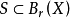 ,那么該集合是有界的(bounded)。
,那么該集合是有界的(bounded)。
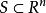
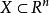
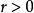
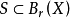
有界的定義可以用某個固定的球心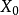 表述,因為如果一個集合包含在球
表述,因為如果一個集合包含在球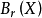 中,那么它也包含在球
中,那么它也包含在球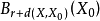 中。我們通常設定
中。我們通常設定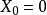 來討論有界性。
來討論有界性。
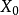
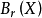
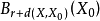
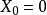
如果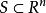 是有界的閉集,那么S是緊集。
是有界的閉集,那么S是緊集。
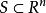
相關概念
定義1 設 是
是 中的一個點序列,設
中的一個點序列,設 為一個正整數序列,並且
為一個正整數序列,並且 [這裡將
[這裡將 寫成
寫成 較為方便]。由
較為方便]。由 組成的序列稱為
組成的序列稱為 的子序列。如果對於所選擇的
的子序列。如果對於所選擇的 ,X“¨,
,X“¨, 收斂,就說序列
收斂,就說序列 有一個收斂的子序列。
有一個收斂的子序列。














相關性質定理
定理1
定理2
如果 是非空(
是非空(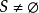 )的緊集,那么S包含了一個最大數和一個最小數。
)的緊集,那么S包含了一個最大數和一個最小數。

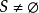
證明: 我們將證明集合S包含一個最大數。證明該集合包含一個最小數的方法是類似的。證明用到了有關實數集R的如下事實:如果一個非空的實數集有上界,那么它有最小上界(實數集S的上界是一個數b,對所有的 有
有 )。也就是說,存在一個數,稱為LUB或者S的上確界(sup),使得如果b是S的任意上界,有b≥sup(S)。假設
)。也就是說,存在一個數,稱為LUB或者S的上確界(sup),使得如果b是S的任意上界,有b≥sup(S)。假設 是非空(
是非空( )的緊集。由於緊集是有界的,因而S有一個最小上界比如說
)的緊集。由於緊集是有界的,因而S有一個最小上界比如說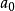 。首先假設
。首先假設 ,那么
,那么 是S中的最大數,否則就不是S的一個上界。接下來假設
是S中的最大數,否則就不是S的一個上界。接下來假設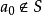 。我們將證明
。我們將證明 是S中點序列的極限,並且,由於S是閉集,因而
是S中點序列的極限,並且,由於S是閉集,因而 一定在S中。這與
一定在S中。這與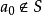 的假設相矛盾。對每一個
的假設相矛盾。對每一個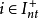 ,存在一個
,存在一個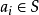 使得
使得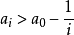 ,否則S將有一個小於
,否則S將有一個小於 的上界。於是
的上界。於是 ,正如我們所要證明的。
,正如我們所要證明的。




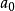


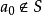


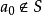
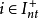
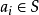
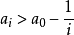


定理3
證明: 只需要證明,如果 是
是 中任意的點序列。那么存在一個收斂於
中任意的點序列。那么存在一個收斂於 中某個點的子序列
中某個點的子序列 根據
根據 的定義,在S中存在點
的定義,在S中存在點 使得對任意的
使得對任意的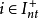 ,有
,有 。由於S是緊集.因而存在
。由於S是緊集.因而存在 的一個子序列,稱之為
的一個子序列,稱之為 使得對
使得對 ,有
,有 。又由於
。又由於 是連續的,
是連續的, 。但由於
。但由於 ,
, 在
在 中。因此
中。因此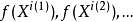 是
是 的收斂於
的收斂於 中一個點的子序列。
中一個點的子序列。






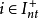










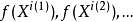


定理4
設S為 的一個非空的緊子集,並設
的一個非空的緊子集,並設 為一個連續函式。則S中存在一個
為一個連續函式。則S中存在一個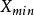 和一個
和一個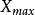 ,使得
,使得


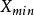
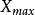


證明:根據定理3, 是緊集;根據定理2,由於
是緊集;根據定理2,由於 ,
, 中存在
中存在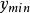 和
和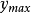 ,使得
,使得