上確界是一個集合的最小上界。
下確界是與上確界相對偶的概念,指的是一個集合的最大下界。
基本介紹
- 中文名:上確界
- 外文名:Supremum
- 概述:一個集合的最小上界
- 序理論:對偶概念是下確界
- 確界定理:實數(連續性)理論基本命題
- 套用領域:序理論 數學分析
定義
序理論
數學分析


常用結論
確界定理
證明










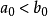








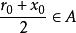


上確界是一個集合的最小上界。
下確界是與上確界相對偶的概念,指的是一個集合的最大下界。












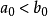








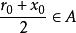


上確界是一個集合的最小上界。下確界是與上確界相對偶的概念,指的是一個集合的最大下界。...
確界原理( supremum and infimum principle )是刻畫實數連續性的命題之一。 設S為非空數集。若S有上界,則S必有上確界;若S有下界,則S必有下確界。 中文名...
若數集S為實數集R的子集有上界,則顯然它有無窮多個上界,而其中最小的一個上界常常具有重要的作用,稱它為數集S的上確界。[1] ...
因為空集當然有上界,我們從有界完全性得出最小元(空界的上確界)的存在性。還要注意儘管術語 "斯科特域"廣泛的用於這個定義,術語"域"沒有一般性意義: 它可以...
,則稱z是x和y的最小上界,也稱為上確界或上端,記為sup(x,y)或 。類似地可以定義x和y的下界,下確界(下端),記為inf(x, y)或 。如果半序線性空間E中任...
上極限是指收斂子數列的極限值的上確界值。...... 上極限數列上極限 給定無窮數列 ,它的一切收斂子數列的極限值的上確界值,稱為該無窮序列的上極限。...
設E是向量格,如果任何有上界的子集都必有上確界,則稱E是序完備的。...... 設E是向量格,如果任何有上界的子集都必有上確界,則稱E是序完備的。...
亦稱保守檢驗。真實水平小於規定顯著性水平的檢驗。檢驗的真實水平指檢驗的第一類錯誤機率的上確界。參見“檢驗水平” ...
並且A對於定向上確界關閉,即,若D是定向集且D CA,則supDEA. (L,a(L))是一個T。拓撲空間.對於任意二任l.,{二}一十二,其中專二~專{川.當1.是連續格...
1.3.3 數集的上確界與下確界習題1.31.4 映射與函式1.4.1 映射與函式的概念1.4.2 函式的表示1.4.3 函式的幾種特性1.4.4 函式的運算...
具體地,對l.= {鎮,U,0,1},設a為語言L的上半格結構類,這些上半格以鎮為偏序,U為上確界運算,0,1分別為最小與最大元.休恩菲爾德猜想的內容是:(R,鎮,...
其中上確界對一切 n 級所有可能的有限多個正整數 取的;由(1) 所規定的‖·‖為 J 上的範數,並且按此範數構成一個巴拿赫空間。巴拿赫空間 J 稱為詹姆斯空間...
若當{Aα}為𝓜+的向上有向族,且 A 為此族的上確界時,總有tr(A)=sup tr(Aα),則稱 tr 為正規跡。有限跡馮·諾伊曼代數 編輯 ...
設𝓕是滿足以下條件的函式族:f(z)在|z|<1解析,f(0)=0,f'(0)=1,對於𝓕中的函式f,β(f)是f(△)所包含的單葉圓的半徑的上確界,則稱B=inf{β(...
極小對的上確界.參考資料 1. 數學辭海 詞條標籤: 科學 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:1次歷史版本 最近更新: 創建者:逐夢天空19...
米歇爾·塔拉格蘭(Michel Talagrand),駐法國索邦大學研究員。 2019年5月,邵逸夫獎基金會授予其數學科學獎,以表彰他研究集中不等式、隨機過程的上確界和自旋玻璃的...
條件備格(conditionally complete lattice)亦稱條件完備格或條件完全格.是備格概念的推廣.若格1中的任意非空有界子集都有上確界和下確界,則稱1為條件備格.許多...
上確界和下確界 1.10 有限覆蓋定理 1.11 上極限和下極限 1.12 Stolz定理 1.13 數列極限的套用第2章 函式的連續性 2.1 集合的映射 2.2 集合的勢 2.3 函式...
[x,y]均為有限偏序集時,稱P為局部有限偏序集.這兩類偏序集是組合理論中的主要研究對象.偏序集上所有鏈的長度的最小上界,或上確界,稱為偏序集的長度,記為l...
完備全序集(complete totally ordered set)一種特殊的全序集.指沒有間隙的全序集.設(屍,<)是稠密全序集.若每個非空有上界的子集ScP,都有上確界,即sups ...
若對於任意UE }l(S),有f-' (U) E }(I ),則稱f為勞森連續函式.函式f;l->S是勞森連續的,若且唯若f保任意下確界與定向上確界.早在1961年,費爾(...
M在m處的局部化Ma、作為局部環R。上有限生成模的維數,記為d(Mm>.取數集{d <Mm ) } m取遍R的極大理想}的上確界,稱為M的維數.設D是微分運算元環,有...
