上確界是一個集合的最小上界。
下確界是與上確界相對偶的概念,指的是一個集合的最大下界。
基本介紹
- 中文名:上確界
- 外文名:Supremum
- 概述:一個集合的最小上界
- 序理論:對偶概念是下確界
- 確界定理:實數(連續性)理論基本命題
- 套用領域:序理論 數學分析
定義
序理論
數學分析


常用結論
確界定理
證明










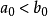








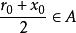


上確界是一個集合的最小上界。
下確界是與上確界相對偶的概念,指的是一個集合的最大下界。












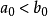








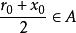


上確界是一個集合的最小上界。下確界是與上確界相對偶的概念,指的是一個集合的最大下界。...
確界原理( supremum and infimum principle )是刻畫實數完備性的命題之一。設S為非空數集。若S有上界,則S必有上確界;若S有下界,則S必有下確界。...
若數集S為實數集R的子集有上界,則顯然它有無窮多個上界,而其中最小的一個上界常常具有重要的作用,稱它為數集S的上確界。[1] ...
上極限是指收斂子數列的極限值的上確界值。...... 上極限數列上極限 給定無窮數列 ,它的一切收斂子數列的極限值的上確界值,稱為該無窮序列的上極限。...
數學上用Sup{}這個記號表示“上確界”,即最小上界。為英文supremum的縮寫。...... 數學上用Sup{}這個記號表示“上確界”,即最小上界。為英文supremum的縮寫。...
在數學中,矩陣或者有界線性運算元的譜半徑是指其特徵值絕對值集合的上確界,一般若為方陣A的譜半徑則寫作ρ(A)。...
格的定義:設(L,≤)是偏序集,若L中任意兩個元素都存在上確界以及下確界,則稱(L,≤)是格(lattice),為了方便,這樣的格成為偏序格。...
波萊爾函式經過有限次的加、減、乘、除運算以及函式的複合,仍然是波萊爾函式;波萊爾函式列的(上、下)極限以及上確界和下確界仍然是波萊爾函式。...
相關詞 上確界,下確界 目錄 1 讀音 2 示例 3 反義詞 上界讀音 編輯 上界(3張) 拼音:shàng jiè英文:upper bound上界示例 編輯 佛家...
稠密:在任意兩個元素之間存在第三個元素 無洞:有上界的非空子集一定有上確界 實數集即為連續統的例子;實際上它是連續統的原型。以下是連續統的幾個例子: 序...
,則稱z是x和y的最小上界,也稱為上確界或上端,記為sup(x,y)或 。類似地可以定義x和y的下界,下確界(下端),記為inf(x, y)或 。如果半序線性空間E中任...
格論是抽象代數的分支,研究格的性質。一個格指的是其任意非空有限子集都有一個上確界(叫並)和一個下確界(叫交)的偏序集合(poset)。...
格的定義:設(L,≤)是偏序集,若L中任意兩個元素都存在上確界以及下確界,則稱(L,≤)是格(lattice),為了方便,這樣的格成為偏序格。...
上確界定義:設S是R中的一個數集,若數η∈S滿足(i)對∀x∈S,有η≥x,即η是S的上界;(ii)對∀a<η,存在x0∈S,使得x0>a,即η是S的最小上界(...
以數學的觀點來看,切比雪夫距離是由一致範數(uniform norm)(或稱為上確界範數)所衍生的度量,也是超凸度量(injective metric space)的一種。...
一個偏序集合是有向完全偏序(dcpo),如果它的每個有向子集都有上確界。完全偏序(cpo)是帶有最小元素的 dcpo。在文獻中,dcpos 有時分類為sup-完全偏序集合,或...
設這一族球的半徑的上確界為R。將這一族按半徑分成子集 ,j為正整數; 包含半徑在區間 的球。依次取 如下:設 。取 為 內互不相交球的子集之中的極大者,...
具體地,對l.= {鎮,U,0,1},設a為語言L的上半格結構類,這些上半格以鎮為偏序,U為上確界運算,0,1分別為最小與最大元.休恩菲爾德猜想的內容是:(R,鎮,...
下極限函式是為判斷函式下半連續性而引進的一個概念。設f(x)是定義在點集E上的擴充實值函式,若在閉包E內的點x的δ鄰域與E的交內,函式f所取的值的下確界...
在數學中,完全布爾代數是所有子集都有上確界的布爾代數。...... 在數學中,完全布爾代數是所有子集都有上確界的布爾代數。完全布爾代數在力迫理論中有重要作用。...
“格”一種特殊的偏序集。在許多數學對象中,所考慮的元素之間具有某種順序。在數學中,完全格是在其中所有子集都有上確界(並)和下確界(交)的偏序集。完全格...
