基本介紹
- 中文名:確界原理
- 外文名:supremum and infimum principle
- 提出者:波爾查諾(Bolzano,B.)
- 提出時間:1817年
- 套用學科:數學
- 適用領域範圍:實數完備性
定義
上界和下界
上確界和下確界

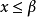






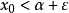

描述
證明




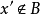





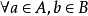


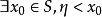



推廣的確界原理
套用














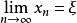
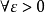




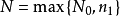



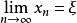

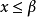






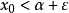





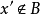





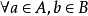


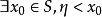

















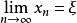
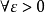




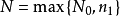



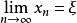
確界原理( supremum and infimum principle )是刻畫實數完備性的命題之一。設S為非空數集。若S有上界,則S必有上確界;若S有下界,則S必有下確界。...
上確界是一個集合的最小上界。下確界是與上確界相對偶的概念,指的是一個集合的最大下界。...
在一般的教科書中,單調有界定理是通過確界原理來證明的,即通過確界原理知道{xn}有上(下)確界α,再證明{xn}收斂於α。事實上,單調有界定理與確界原理等價,...
而閉區間上連續函式的有界性定理的證明,在很多數學教材中,有多種方法可以證明此定理。比如可以利用閉區間套定理、確界定理、單調有界定理和柯西收斂準等。我們知道...
有界函式並不一定是連續的。根據定義,ƒ在D上有上(下)界,則意味著值域ƒ(D)是一個有上(下)界的數集。根據確界原理,ƒ在定義域上有上(下)確界。一...
但這裡有一個很微妙的問題,即與連續性公理等價的7個實數系的基本定理(確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂...
由戴德金定理證明非空有上界數集必有上確界,非空有下界數集必有下確界同理。設S為一非空有上界數集,即 成立。取數集B為S所有上界的集合,A=R/B。則:...
最小上界公理,又稱為上確界原理,是實分析的公理。之所以稱為公理,是因為它在實分析的公理系統里,不能被除了它本身以外的公理所證明。這個公理聲稱如果實數的非...
確界原理:若集合M有上界,則必有上確界;若集合M有下界,則必有下確界。[2] 上確界定義:設S是R中的一個數集,若數η∈S滿足...
作為柯西收斂準則的套用之一,我們可以用來證明實數的確界原理。確界原理:非空有上(下)界數集,必有上(下)確界。證明:先證非空有上界數集必有上確界。...
證明:利用確界原理:非空有上(下)界的點集必有上(下)確界。由於已經證明了f(x)在[a,b]上有界,因此由確界原理可知,f(x)的值域f([a,b])必有上確界...
這裡把戴德金定理用作連續性公理。另一個常用作連續性公理的確界原理。公理組I~III與公理組I+II+(III)’是等價的,(注意不是III<=>(III)’)。完備性公理...
非構造方法對於康托爾集合論和數學分析有本質的意義,因之戴德金德分割、 上確界定理和波爾察諾-魏爾施特拉斯定理等都失去根據。古典數學的這些部分必須改造或被...
5、有沒有人認為洛必達法則和皮亞諾餘項的泰勒公式和確界原理是沒有關係的?看來在座的沒有我的信徒啊。那你們期末考試全部不及格6、要么我們搞個顧氏定理,...
