基本介紹
- 中文名:三角不等式
- 外文名:the Triangle Inequality
- 套用學科:理工
- 適用領域範圍:數學、物理
- 學科領域:數學,平面幾何
- 基本解釋:在三角形中兩邊之和大於第三邊
內容及其證明
內容
證明
設ABC為一個三角形,記△ABC,延長BA至點D,使DA = CA,連線DC.

推論
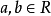


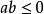
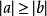



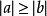
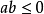


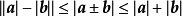
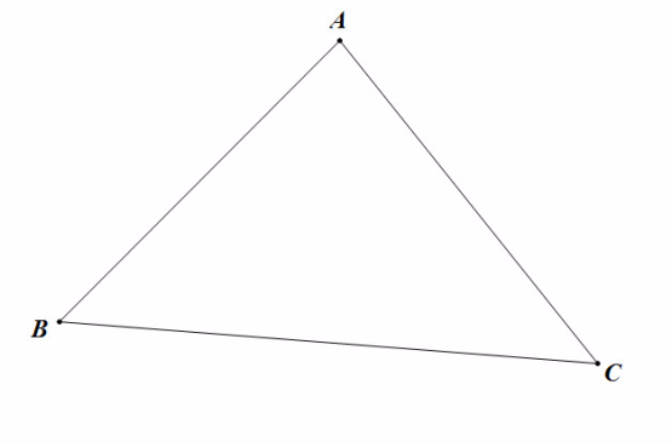

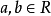


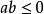
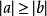



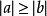
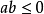


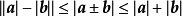
三角不等式,即在三角形中兩邊之和大於第三邊,有時亦指用不等號連線的含有三角函式的式子(這裡不作介紹)。三角不等式雖然簡單,但卻是平面幾何不等式里最為基礎...
三角形不等式(triangular inequality)可以指三角形邊長關係的不等式,也可以指三角形邊長關係的推廣,即以三角形邊長關係的不等式這一幾何事實為背景的不等式。...
最簡三角不等式(simplest trigonometric inequality)亦稱基本三角不等式,指形如f(x)>m的不等式,其中f(x)是已知三角函式,解三角不等式是求出使不等式成立的所有解...
《三角不等式及其套用》是2013年中國科學技術大學出版社出版的圖書,作者是張運籌。...... 《三角不等式及其套用》是2013年中國科學技術大學出版社出版的圖書,作者是...
《三角不等式及其套用(第2版)》是2013年出版的圖書,作者是張運籌。...... 《三角不等式及其套用(第2版)》是2013年出版的圖書,作者是張運籌。書名 三角不等式及...
在數學中,閔可夫斯基不等式(Minkowski inequality)是德國數學家赫爾曼·閔可夫斯基提出的重要不等式,該不等式表明Lp空間是一個賦范向量空間。閔可夫斯基的主要工作在...
距離空間(X,d)中的距離d滿足三角不等式的加強形式,稱為“超距不等式”。...... 距離空間(X,d)中的距離d滿足三角不等式的加強形式,稱為“超距不等式”。...
在數學中,閔可夫斯基不等式(Minkowski inequality)表明LP空間是一個賦范向量空間。...... 閔可夫斯基不等式是 中的三角不等式。它可以用赫爾德不等式來證明。和赫爾...
數學上,柯西-施瓦茨不等式,又稱施瓦茨不等式或柯西-布尼亞科夫斯基-施瓦茨不等式,是一條很多場合都用得上的不等式;例如線性代數的矢量,數學分析的無窮級數和乘積的...
在數學裡的泛函分析中,貝塞爾不等式是類似於勾股定理的一種不等式。貝塞爾不等式揭示了希爾伯特空間中的一個元素和它在一個正交序列上的投影之間的關係。舉例來說,...
範數(norm)是數學中的一種基本概念。在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次性;③三角不等式。它常常被用來度量某個向量...
