最簡三角不等式(simplest trigonometric inequality)亦稱基本三角不等式，指形如f(x)>m的不等式，其中f(x)是已知三角函式，解三角不等式是求出使不等式成立的所有解的集合。
基本介紹
- 中文名：最簡三角不等式
- 外文名：simplest trigonometric inequality
- 別稱：基本三角不等式
- 所屬學科：數學
- 所屬問題：平面三角(三角方程與三角不等式)
基本介紹,最簡三角不等式的幾何意義,例題解析,最簡三角不等式的解集,
基本介紹
最簡三角不等式亦稱基本三角不等式，含有變元的基本三角不等式，若f(x)是基本三角函式，則f(x)>m或f(x)<m(m∈R)稱為最簡三角不等式。
最簡三角不等式的幾何意義
最簡三角不等式的幾何意義是單位圓上滿足不等式的角的範圍。從函式y=sinx的圖象也容易理解三角不等式的幾何意義。
圖1例題解析
解下列不等式。
(1)2sinx－1≤0； (2)
；
解 (1)原不等式可化為
，由於y=sinx的最小正周期為2π，因此可以先在[0,2π]內求出不等式的解集，利用單位圓正弦函式線，得
圖2所以，原不等式的解集為
(2)原不等式可化為
，由於
的最小正周期為2π，因此可以先在[－π，π]內求出不等式的解集，利用單位圓餘弦線，得
。
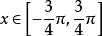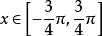
圖3所以，原不等式的解集為
最簡三角不等式的解集
最簡三角不等式的解集列表如下(表中k∈Z)：
不等式 | a的取值域 | 不等式的解集 |
sinx>a | a< -1 | R |
-1≤a<1 | 2kπ+arcsin a<x<(2k+1)π-arcsin a | |
a≥1 | ∅ | |
sin x | a≤-1 | ∅ |
-1<a≤1 | (2k-1)π-arcsin a<x<2kπ+arcsin a | |
a>1 | R | |
cos x>a | a<-1 | R |
-1≤a<1 | 2kπ-arccos a<x<2kπ+arccos a | |
a≥1 | ∅ | |
cos x | a≤-1 | ∅ |
-1<a≤1 | 2kπ+arccos a<x<(2k+1)π-arccos a | |
a>1 | R | |
tanx>a | R | kπ+arctan a<x<kπ+π/2 |
tan x | R | kπ-π/2<x<kπ+arctan a |
cot x>a | R | kπ+arccot a<x<kπ+π/2 |
cot x | R | kπ-π/2<x<kπ+arccot a |
