相關詞條
- 單位圓
單位圓指的是平面直角坐標繫上,圓心為原點,半徑為單位長度的圓...... (−x)2,並且所有這些點相對於x軸或者y軸的反射點也都位於單位圓上,因此單位圓上的所有...
- 機關單位園林綠地設計
《機關單位園林綠地設計》是2002年中國林業出版社出版的圖書,作者是蔣桂香、李珂、孟瑾、和祥、陳濤。...
- 正切線
三角函式線之一。在平面直角坐標系內,以原點為中心,做一個半徑為單位長度的單位圓.做過圓和x軸交點的切線.則,從原點引出的一條射線,與這條切線的交點,到x軸...
- 圓函式
圓函式即三角函式,是一類基本初等函式的總稱,可以通過一個單位圓來定義一系列函式。因三角函式的研究曾經長期在單位圓內進行,由此而得名。...
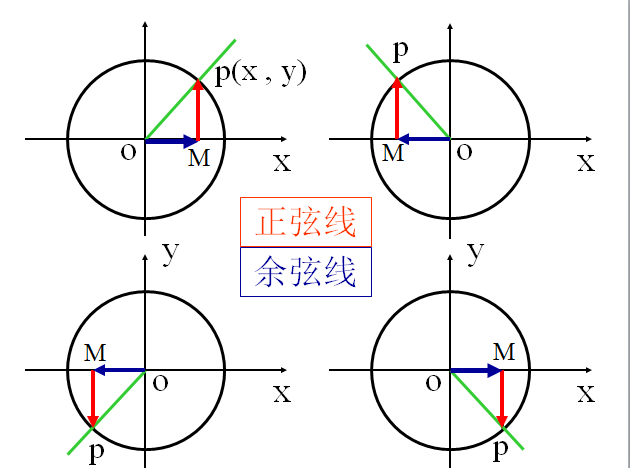
- 正弦
一般的,在直角坐標系中,給定單位圓,對任意角α,使角α的頂點與原點重合,始邊與x軸非負半軸重合,終邊與單位圓交於點P(u,v),那么點P的縱坐標v叫做角α的正...
- 正割
在單位圓上,正割函式位於割線上,因此將此函式命名為正割函式。 和其他三角函式一樣,正割函式一樣可以擴展到複數。 中文名 正割 外文名 Secant 值域 絕對值大於...
- sin函式
對於大於 2π 或小於 0 的角度,簡單的繼續繞單位圓旋轉。在這種方式下,正弦變成了周期為 2π的周期函式。sin函式基本性質 編輯 ...
- 餘割函式
設一個過原點的線,同x軸正半部分得到一個角θ,並與單位圓相交。這個交點的y坐標等於sinθ。在這個圖形中的三角形確保了這個公式;半徑等於斜邊並有長度1,所以有...
- 克貝1/4定理
克貝1/4定理是關於S類函式映射性質的一個定理。該定理斷言:若f∈S,則單位圓盤在f映射下的像包含以原點為中心以1/4為半徑的圓盤。...
- 圓盤代數
設T為複平面中單位圓周,圓盤代數是C(T)中的可以連續擴張成單位開圓內的解析函式全體所構成的閉子代數A。...
- 正交矩陣
如果AAT=E(E為單位矩陣,AT表示“矩陣A的轉置矩陣”)或ATA=E,則n階實矩陣A稱為正交矩陣。正交矩陣是實數特殊化的酉矩陣,因此總是屬於正規矩陣。儘管我們在這裡...