基本介紹
研究歷史

三角函式

正弦函式
平方和關係
積的關係
倒數關係
商的關係
和角公式
倍角半角公式
正弦定理
正弦定理
單位圓
級數


微分方程

正弦積分
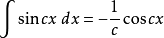








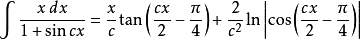


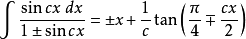
恆等變換
函式 |  | 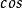 |  |  |  |  |
 |  | 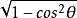 |  |  |  |  |



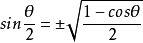
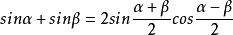
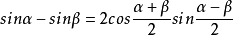

數學術語
拉普拉斯變換







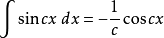








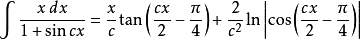


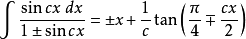
函式 |  | 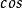 |  |  |  |  |
 |  | 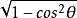 |  |  |  |  |



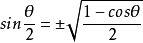
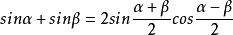
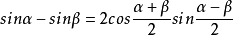


正弦(sine),數學術語,在直角三角形中,任意一銳角∠A的對邊與斜邊的比叫做∠A的正弦,記作sinA(由英語sine一詞簡寫得來),即sinA=∠A的對邊/斜邊。古代說法,...
正弦曲線或正弦波(Sinusoid/Sine wave)是一種來自數學三角函式中的正弦比例的曲線。也是模擬信號的代表,與代表數位訊號的方波相對。正弦曲線可表示為y=Asin(ωx+φ...
正弦值是在直角三角形中,對邊的長比上斜邊的長的值。 任意銳角的正弦值等於它的餘角的餘弦值,任意銳角的餘弦值等於它的餘角的正弦值。...
大小和方向隨時間作有規律變化的電壓和電流稱為交流電,又稱交變電流。正弦交流電是隨時間按照正弦函式規律變化的電壓和電流。由於交流電的大小和方向都是隨時間不...
正弦電流(sine-wave current)指按正弦規律隨時間變化的交變電流,工程上常用正弦電流和電壓的有效值表示其大小。...
正弦公式是描述正弦定理的相關公式,而正弦定理是三角學中的一個基本定理,它指出:在任意一個平面三角形中,各邊和它所對角的正弦值的比相等且等於外接圓的直徑。...
正弦積分是由積分定義的一種特殊函式。英文翻譯為sine integral,常用語計算正弦積分函式值,在性質上常與餘弦積分作比較。...
反正弦函式簡介 編輯 在數學中,反三角函式(偶爾也稱為弓形函式(arcus functions),反向函式(antitrigonometric functions)或環形函式(cyclometric functions)是三角函式...
一般來說,一個函式的傅立葉級數既含有正弦項,又含有餘弦項。特別地,只含有正弦項的傅立葉級數稱為正弦級數,只含有餘弦項的傅立葉級數稱為餘弦級數。...
正弦型函式是形如y=Asin(ωx+φ)+k的函式,其中A,ω,φ,k是常數,且ω≠0。函式y=Asin(ωx+φ),(A>0,ω>0),x∈R的圖象可以看作是用下面的方法得到...
正弦波是頻率成分最為單一的一種信號,因這種信號的波形是數學上的正弦曲線而得名。任何複雜信號——例如音樂信號,都可以看成由許許多多頻率不同、大小不等的...
正弦定理(The Law of Sines)是三角學中的一個基本定理,它指出“在任意一個平面三角形中,各邊和它所對角的正弦值的比相等且等於外接圓的直徑”,即a/sinA = ...
雙曲正弦函式是雙曲函式的一種。雙曲正弦函式在數學語言上一般記作sinh,也可簡寫成sh。與三角函式一樣,雙曲函式也分為雙曲正弦、雙曲餘弦、雙曲正切、雙曲...
正弦波變數正弦波頻率成分最為單一的一種信號,因這種信號的波形是數學上的正弦曲線而得名。任何複雜信號——例如音樂信號,都可以看成由許許多多頻率不同、大小不...
正弦信號是頻率成分最為單一的一種信號,因這種信號的波形是數學上的正弦曲線而得名。工業及照明用電就是正弦信號。振盪電路輸出的正弦波一般都含有諧波分量,方波就...
2. 正弦、餘弦定理在三角形中的套用 .中國知網[引用日期2017-11-27] 3. 正餘弦定理、三角形的一些公式 .百度文庫[引用日期2017-11-27] 4. 建議先講授"餘弦...
若將α看成銳角(終邊在第一象限),則π-α是第二象限的角(終邊在第二象限),正弦函式的三角函式值在第二象限是正值,餘弦函式的三角函式值在第二象限是負值,正...
正弦函式 sinθ=y/r餘弦函式 cosθ=x/r正切函式 tanθ=y/x餘切函式 cotθ=x/y正割函式 secθ=r/x餘割函式 cscθ=r/y正切同角三角函式 ...
反三角函式是一種基本初等函式。它是反正弦arcsin x,反餘弦arccos x,反正切arctan x,反餘切arccot x,反正割arcsec x,反餘割arccsc x這些函式的統稱,各自表示...
正餘弦定理指正弦定理和餘弦定理,是揭示三角形邊角關係的重要定理,直接運用它可解決三角形的問題,若對餘弦定理加以變形並適當移於其它知識,則使用起來更為方便、...
