基本介紹
- 中文名:拉普拉斯變換
- 外文名:Laplace Transform
- 別稱:拉氏變換
- 提出者:拉普拉斯
- 提出時間:約1812年
- 套用學科:數學、工程數學
- 適用領域範圍:解微分、積分方程,偏微分方程
- 適用領域範圍:信號系統、電子工程、軌道交通、自動化等
公式概念
拉普拉斯變換的公式

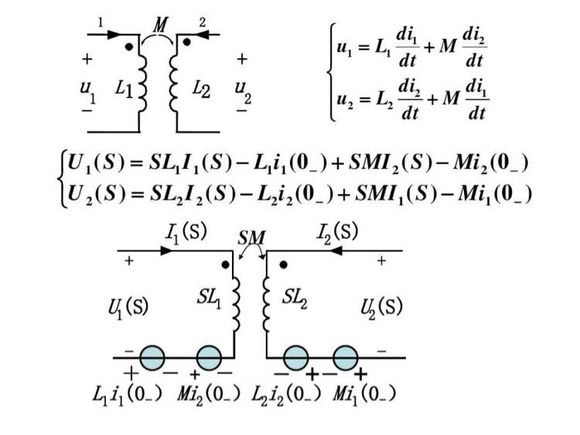
電路分析實例


拉普拉斯逆變換

意義與作用
基本性質



發展歷史
與傅立葉變換的聯繫



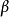










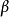


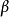









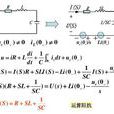











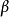










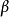


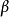









拉普拉斯變換是工程數學中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有參數實數t(t≥ 0)的函式轉換為一個參數為複數s的函式。拉普拉斯...
拉普拉斯變換法(method of Laplace transform)求解常係數線性常微分方程的一個重要方法。運用拉普拉斯變換將常係數線性常微分方程的求解問題化為線性代數方程或方程組...
拉普拉斯逆變換為當已知信號函式x(t)的拉普拉斯變換X(s),求解信號的時域表達式x(t)。...
雙邊拉普拉斯變換是一種積分變換,作用對象是任意實數t的實數函式或是複變函數 f(t),作用結果是F(s),其形式類似機率中的動差生成函式,雙邊拉普拉斯變換和傅立葉...
雙側拉普拉斯變換(bilateral Laplace transformation)是一種積分變換,作用對象是任意實數t的實數函式或是複變函數 f(t),作用結果是F(s),其形式類似機率中的動差...
拉普拉斯變換是工程數學中常用的一種積分變換。...... 左端的定積分稱為拉普拉斯積分,又稱為f(t)的拉普拉斯變換;右端的F(S)是拉普拉斯積分的結果,此積分把時域中...
拉普拉斯方程(Laplace's equation)又稱調和方程、位勢方程,是一種偏微分方程,因由法國數學家拉普拉斯首先提出而得名。拉普拉斯方程表示液面曲率與液體表面壓強之間的...
內容介紹本教材內容包括級數和拉普拉斯變換,每章前有學習指南,章後有本章小結和數學實驗,便於學生自學,教材內容充實,結構合理,在敘述上既注重知識的體系,又注重理論...
拉普拉斯變換(英文:Laplace Transform),是工程數學中常用的一種積分變換。...... 拉普拉斯變換(英文:Laplace Transform),是工程數學中常用的一種積分變換。...
拉普拉斯(Pierre-Simon Laplace,1749-1827)是法國分析學家、機率論學家和物理學家,法國科學院院士。1749年3月23日生於法國西北部卡爾瓦多斯的博蒙昂諾日,1827年3...
在數學中,梅林變換是一種以冪函式為核的積分變換。...... 雙邊拉普拉斯變換可以用梅林變換 [1] 來表示,如下式梅林變換也可以用雙邊拉普拉斯變換來表示,如下式...
皮埃爾-西蒙·拉普拉斯侯爵(Pierre-Simon marquis de Laplace,1749年3月23日-1827年3月5日),法國著名的天文學家和數學家,也是法國科學院院士。他是天體力學的主要...
定義式如下:Mellin 變換有許多套用,例如可以證明黎曼ζ函式的函式方程。 在數學中,梅林變換是一種積分變換,可以被視為雙邊拉普拉斯變換的乘法版本。這個積分變換與...
《教育部高職高專規劃教材:級數與拉普拉斯變換》是2003年9月1日 化學工業出版社出版的圖書,作者是韓志剛。...
用變換方法,把解微分方程的問題變換為解代數方程的問題,從而轉化為較初等的數學運算.現代數學中許多變換問題已成了專門的研究課題,例如拉普拉斯變換、傅立葉變換等....
但不論其如何發展,都是以最簡單的傅立葉變換為基礎,只要掌握傅立葉變換的基礎理論,便可以進一步套用更多形式的傅立葉變換方法。數學變換方法拉普拉斯變換 ...
拉普拉斯變換的重要性質包括:尺度變換、時移、頻移、微分、積分、卷積、初值定理與終值定理,與其他性質相比,初值定理與終值定理是重點和難點 [1] 。Z域分析的終值...
拉普拉斯變換的重要性質包括:尺度變換、時移、頻移、微分、積分、卷積、初值定理與終值定理,與其他性質相比,初值定理與終值定理是重點和難點 [1] 。 從物理意義上...
傳遞函式是指零初始條件下線性系統回響(即輸出)量的拉普拉斯變換(或z變換)與激勵(即輸入)量的拉普拉斯變換之比。記作G(s)=Y(s)/U(s),其中Y(s)、U(s)...
對復參數s,函式f(t)*e^(-st)在(-∞,+∞)的積分,稱為函式f(t)的(雙邊)拉普拉斯變換,簡稱拉氏變換(如果是在[0,+∞)內積分,則稱為單邊拉普拉斯變換,記...
