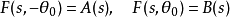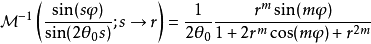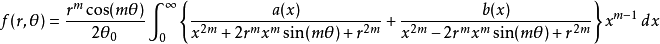基本介紹
- 中文名:梅林變換
- 外文名:Mellin transform
- 分類:積分變換、複分析
- 領域:數理科學
定義,與其他變換之關係,雙邊拉普拉斯變換,傅立葉變換,範例,Cahen–Mellin 積分,數論,圓柱坐標系下的拉普拉斯運算元,
定義
定義式如下:
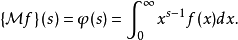
而其逆變換為
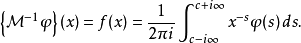
與其他變換之關係
雙邊拉普拉斯變換
雙邊拉普拉斯變換可以用梅林變換來表示,如下式
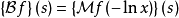
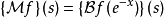
傅立葉變換
傅立葉變換可以用梅林變換來表示,如下式

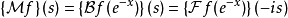
範例
Cahen–Mellin 積分
對於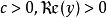 ,且
,且 在主要分支(principal branch)上,我們有
在主要分支(principal branch)上,我們有
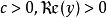

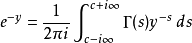

數論
假設

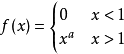
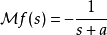
圓柱坐標系下的拉普拉斯運算元
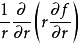
例如,拉普拉斯運算元在二維空間的極坐標表示法
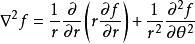


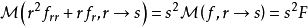
舉例來說,二維拉普拉斯方程的極坐標表示法具有以下形式


利用梅林變換,可以轉換成一個簡諧振子的形式

通解為:

給定邊界條件

其梅林變換為