積分變換的定義
通過參變數積分將一個已知函式變為另一個函式。已知ƒ(x),如果
存在(其中,α、b可為無窮),則稱F(s)為ƒ(x)以K(s,x)為核的積分變換。
典型積分變換
積分變換無論在數學理論或其套用中都是一種非常有用的工具。最重要的積分變換有
傅立葉變換、
拉普拉斯變換,此外還有梅林變換和漢克爾變換,它們都可通過傅立葉變換或拉普拉斯變換轉化而來。傅立葉變換和拉普拉斯變換的詳細介紹參考相關詞條,這裡就不再贅述。
梅林變換
當K(s,x)=xs_1,x>0,而ƒ(x)定義於[0,+∞),函式(式(1)):
稱為
ƒ(
x)的梅林變換,式中
s=
σ+iτ為
複數。M(
s)的梅林反變換則定義為(式(2)):
這裡積分是沿直線Res=σ進行的。
(1)式與(2)式在一定條件下互為
反演公式。例如,設(1)
絕對收斂,在任何有限區間上
ƒ(
x)是有界變差的,且已規範,則由(1)可推得(2),在
l2(0,∞)空間中也有類似結果。
若以M(s,ƒ′)表示ƒ′(x)的梅林變換,則在一定條件下,有:
式中с>Res。
 積分變換
積分變換漢克爾變換
設
Jγ(
x)為у階
貝塞爾函式(見
特殊函式),
ƒ(
x)定義於[0,+∞),則稱(式(3)):
為ƒ(x)的у階漢克爾變換;而稱(式(4)):
為h(t)的漢克爾反變換。有的作者代替(3)與(4)改用 與
效果是一樣的。在一定條件下,(3)與(4)成為一對互逆公式,此外,還有:
 積分變換
積分變換積分的分類
(1)
定積分:設
閉區間[a,b]上有n-1個點,依次為a=x0<x1<x2…<xn-1<xn=b,它們把[a,b]分成n個小區間△i=[xi-1,xi],i=1,2,…,n.這些分點或這些閉子區間構成對[a,b]的分割,記為T={x0,x2,…,xn}或{△1,△2,…△n},小區間△i的長度為△xi=△xi-△xi-1,並記‖T‖=MAX{△Xi},稱為分割T的模。
(4)重積分;
同名圖書《積分變換》
內容簡介
本書是由刁元勝編著的。本書介紹了如何用積分變換的方法來簡化數學問題中難以求解的問題。積分變換是通過積分的方法,把一個函式變換為另一個函式。對不同的變換選取不同的形式。這種變換是一一對應的,否則做逆變換的時候就不能得到唯一的解,不符合工程上解得
唯一性原則,這樣,積分變換就不具有實用價值。
目錄
傅立葉變換
1.1 傅立葉積分和傅立葉變換
1.2 單位脈衝函式
1.3 傅立葉變換的性質
1.4 能量積分與相關函式
1.5 傅立葉變換在數理方程中的套用
拉普拉斯變換
2.1 拉普拉斯變換的概念
2.2 拉普拉斯變換的性質
2.3 拉普拉斯逆變換
2.4 拉普拉斯變換的套用
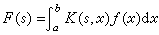
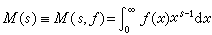

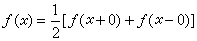
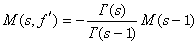
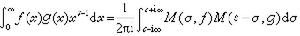
 積分變換
積分變換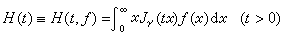



 積分變換
積分變換
