基本介紹
解釋
性質




求解

積分公式















 不定積分
不定積分積分方法
積分公式法
換元積分法
 不定積分
不定積分





分部積分法
 不定積分
不定積分不可積函式

 不定積分
不定積分積分表


示例


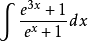





















 不定積分
不定積分 不定積分
不定積分





 不定積分
不定積分
 不定積分
不定積分



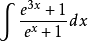

在微積分中,一個函式f 的不定積分,或原函式,或反導數,是一個導數等於f 的函式 F ,即F′ = f。不定積分和定積分間的關係由微積分基本定理確定。其中F是f...
不定積分的積分公式主要有如下幾類:含ax+b的積分、含√(a+bx)的積分、含有x^2±α^2的積分、含有ax^2+b(a>0)的積分、含有√(a²+x^2) (a>0)...
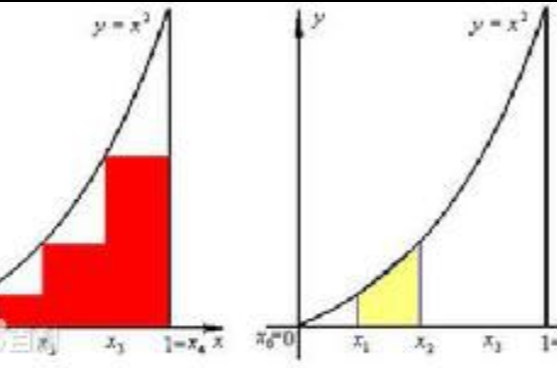
定積分是積分的一種,是函式f(x)在區間[a,b]上積分和的極限。這裡應注意定積分與不定積分之間的關係:若定積分存在,則它是一個具體的數值(曲邊梯形的面積),...
不定積分的運算法則,別稱不定積分的性質,f(x)的原函式,存在微分的反函式。...... 不定積分的運算法則,別稱不定積分的性質,f(x)的原函式,存在微分的反函式。...
不定積分是微分的逆運算。...... 不定積分是微分的逆運算。所以我們得到一些基本的公式:詞條標籤: 科技術語 , 科學 V百科往期回顧 詞條統計 瀏覽次數:次 編輯...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
狹義當儒瓦不定積分狹義當儒瓦可積函式 狹義當儒瓦可積函式是勒貝格可積函式的推廣。當儒瓦(Denjoy,A.)於1912年給出了狹義當儒瓦積分的定義,它同時成為勒貝格積分和...
勒貝格不定積分簡介 編輯 勒貝格積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的...
積分表是在積分計算中為了使用與方便,把常用的積分公式匯集成的一種數學用表。積分表是按照被積函式的類型來排列的。求積分時,可根據被積函式的類型直接地或經過...
分部積分法是微積分學中的一類重要的、基本的計算積分的方法。它是由微分的乘法法則和微積分基本定理推導而來的。它的主要原理是將不易直接求結果的積分形式,轉化...
換元積分法(Integration By Substitution)是求積分的一種方法,主要通過引進中間變數作變數替換使原式簡易,從而來求較複雜的不定積分。它是由鏈式法則和微積分基本...
如果上限x在區間[a,b]上任意變動,則對於每一個取定的x值,定積分有一個對應值,所以它在[a,b]上定義了一個函式,這就是積分變限函式。...
因此,對於證明有關題設中含有某個函式積分的等式或不等式,或者要證的結論中含有定積分,或者所求的極限式中含有定積分時,一般應考慮使用積分中值定理, 去掉積分號...
現行不定積分的定義為:若函式f(x)在某區間 I 上存在一個原函式F(x),則稱F(x)+C(C為任意常數)為f(x)在該區間上的不定積分,記為 。...
有理函式積分法是按一定步驟求有理函式不定積分的方法,求有理函式的積分時,先將有理式分解為多項式與部分分式之和,再對所得到的分解式逐項積分。有理函式的原...
《常用積分表》包含最常用的初等函式和特殊函式的不定積分與定積分公式2552個,另外還有203個積分變換公式.積分公式中遇到的所有函式(包括被積函式和積分後的函式)的...
1 定義 2 基本積分表 3 換元積分法 4 分部積分法 積分法定義 編輯 積分法是從已知函式f求其原函式(不定積分)的方法。包括(...
二重積分是二元函式在空間上的積分,同定積分類似,是某種特定形式的和的極限。本質是求曲頂柱體體積。重積分有著廣泛的套用,可以用來計算曲面的面積,平面薄片重心等...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
極坐標定積分是以R為半徑,θ為積分變元,計算曲線周長的、面積的積分。曲線的周長定積分為,曲線的面積定積分為。設曲線ρ=R在區間[θ1,θ2]上非負連續,當d...
積分不等式是微積分學中的一類重要不等式,也為解決微分方程等方面的問題提供了 富有成效的理論工具。主要有楊不等式,施瓦茲不等式,閔可夫斯基不等式,延森不等式等...
在某些積分中,可以將含有三角函式的積分變為有理分式的積分。 [1] 總結:因此,這組公式被稱為以切表弦公式,簡稱以切表弦。它們是由二倍角公式變形得到的。而...
不定積分的換元法解法整體換元 又稱整體換元,是在已知或者未知中,某個代數式幾次出現,而用一個字母來代替它從而簡化問題,當然有時候要通過變形才能發現。例如解...
