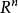積分不等式是微積分學中的一類重要不等式,也為解決微分方程等方面的問題提供了 富有成效的理論工具。主要有楊不等式,施瓦茲不等式,閔可夫斯基不等式,延森不等式等。
基本介紹
- 中文名:積分不等式
- 外文名:integral inequality
- 舉例:楊不等式、施瓦茲不等式等
- 類型:數學術語
- 隸屬:微積分學
楊不等式,施瓦茲不等式,閔可夫斯基不等式,延森不等式,
楊不等式
有關函式及其反函式積分的不等式。設f在 上連續,且嚴格增,
上連續,且嚴格增, ,則對任意的a≥0及
,則對任意的a≥0及












 圖1楊不等式的幾何意義
圖1楊不等式的幾何意義從楊不等式可以得到一些有用的不等式,如 (也有人稱為楊不等式),其中1/p+1/q=1,p>1,q>1,a,b≥0,等號若且唯若
(也有人稱為楊不等式),其中1/p+1/q=1,p>1,q>1,a,b≥0,等號若且唯若 時成立。若f:
時成立。若f: →
→ ,右連續且增,
,右連續且增,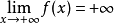 ,則f(x)稱為楊函式。若對楊函式f(x),定義其右反函式
,則f(x)稱為楊函式。若對楊函式f(x),定義其右反函式 為:y∈[0,f(0)]時,
為:y∈[0,f(0)]時,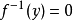 ;而
;而 時,
時, 。則對a,b≥0,有
。則對a,b≥0,有




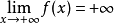

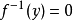


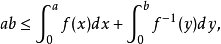


楊不等式可以推廣(1989)為






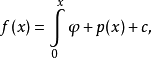


施瓦茲不等式
赫爾德不等式中用得最普遍的是p=q=2的情況,此時的赫爾德不等式稱為施瓦茲不等式,有時也稱為柯西不等式或布尼亞科夫斯基不等式。
見施瓦茲不等式。
閔可夫斯基不等式
(1)對所有的正實數 有
有









(3)序列形式的閔可夫斯基不等式。
設 為兩個實數列,滿足條件
為兩個實數列,滿足條件






延森不等式
有關凸函式的一個不等式。它的離散形式是

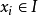



延森不等式的積分形式是





以上不等式中,I可以換成凸集(這時積分應為勒貝格積分)。當f是凹函式時不等號反向。適當地選擇f, 或函式q,可以得到許多著名的不等式。例如,取f(x)=-ln x(x>0)及
或函式q,可以得到許多著名的不等式。例如,取f(x)=-ln x(x>0)及 ,可以得到平均不等式與赫爾德不等式。離散形式的延森不等式是赫爾德(Ho¨lder,O.L.)於1889年得到的,積分形式是延森(Jensen,J.L.W.V.)於1906年建立的。
,可以得到平均不等式與赫爾德不等式。離散形式的延森不等式是赫爾德(Ho¨lder,O.L.)於1889年得到的,積分形式是延森(Jensen,J.L.W.V.)於1906年建立的。