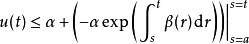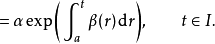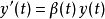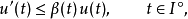Gronwall不等式

Gronwall不等式是目前常用不等式之一。它與Holder不等式一樣，分別具備離散形式與連續形式。

在數學中，格朗沃爾引理或格朗沃爾不等式說明了對於滿足一定的微分方程或積分方程的函式，有相應的關於此微分方程或積分方程的不等式。格朗沃爾不等式有兩種形式，分別是積分形式和微分形式。積分形式下的不等式可以有幾種不同的寫法。

基本介紹

• 中文名：格朗沃爾不等式
• 外文名：Gronwall's inequality
• 提出者：瑞典的數學家格朗沃爾
• 套用學科：數學
• 適用領域範圍：數學
• 形式：積分形式和微分形式

釋義

在數學中，格朗沃爾引理或格朗沃爾不等式說明了對於滿足一定的微分方程或積分方程的函式，有相應的關於此微分方程或積分方程的不等式。格朗沃爾不等式有兩種形式，分別是積分形式和微分形式。積分形式下的不等式可以有幾種不同的寫法。

格朗沃爾不等式常常被用來估計常微分方程的解的取值範圍。比如，它可以用來證明初值問題的解的唯一性（見柯西-利普希茨定理）。

格朗沃爾不等式的名稱來自多瑪·哈肯·格朗沃爾。格朗沃爾是一位瑞典的數學家，後來移居美國。

格朗沃爾不等式的微分形式首先由格朗沃爾在1919年證明。而積分形式則是由理察·貝爾曼（Richard Bellman）在1943年證明。

離散形式

設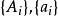 是非負實數列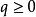， 。如果對每一個 ，

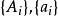
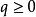
那么

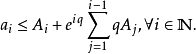
連續形式

設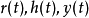 是定義在 上的連續實函式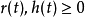， 。如果對一切 ，都有

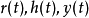
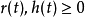
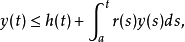
那么

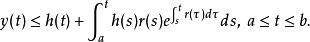
微分形式

設I是一個實數區間，記為：[a,∞) 或 [a,b] 或 [a,b)，其中a<b。又設β和u為定義在I上的實數值的連續函式。假設u是一個在I的內部（也就是不包括端點）可微的函式，並且滿足如下的微分不等式：

那么對於所有的 ，函式u都小於等於以下微分方程的解：

注意：不等式對函式β和u的符號沒有任何要求。

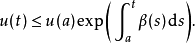
證明

如果設

是以下微分方程

其中v(a)= 1 的解，那么對所有的t都有v(t)> 0， 因此根據複合函式求導法則中的除法定則：

對所有的t>a成立，因此

於是格朗沃爾不等式得證。

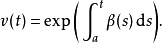
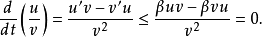
積分形式

設I是一個實數區間，記為：[a,∞) 或 [a,b] 或 [a,b)，其中a<b。又設α、β和u為定義在I上的實數值的函式。假設β和u是連續的，則有：

(a) 如果β是非負函式並且u滿足如下的積分不等式：

，

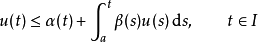
那么

。

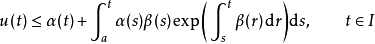
(b) 如果在之前的條件下，α還是一個常數，那么

注意：

不等式的成立條件里並沒有限制α和u的符號；

相比於微分形式，積分形式中對函式u的可微性沒有做要求。

證明

(a) 定義

則運用複合函式求導法則中的乘積法則、鏈式法則、指數函式的求導法則以及微積分基本定理，可以得到：

由於注意到括弧中的部分小於α，可以得到相應的不等式，並進行積分。由於函式β以及其指數都是非負函式，積分後不等號保持不變。然而v(a)=0，因此積分式等價於：

再運用第一步里v(t) 的定義，就得到：

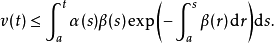
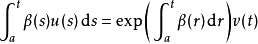
最後將原來條件里的不等式帶入上式左邊，就可以得到格朗沃爾不等式了。

(b) 如果函式α為常數函式，那么命題 (a) 中不等式的右邊可以進行積分。由微積分基本定理可以獲得：