定義
數學上,集合
S 的
內部(又稱
開核)含有所有直觀上“不在
S 的邊界上”的
S 的
點。
S 的內部中的點稱為
S 的
內點。
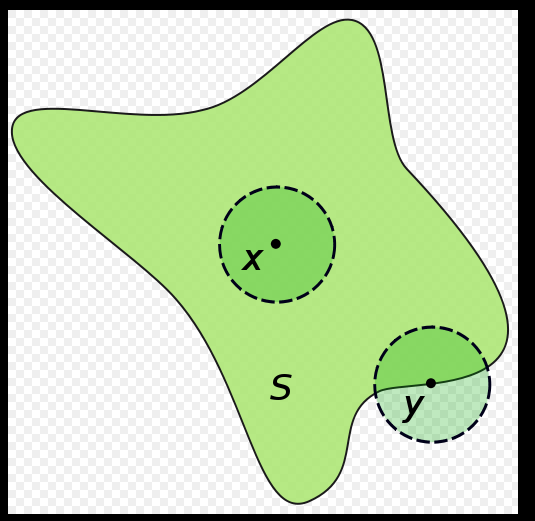
若
S 為
歐幾里德空間的子集,則
x 是
S 的內點,若存在以
x 為中心的
開球被包含於
S。
這個定義可以推廣到
度量空間X 的任意子集
S。具體地說,對具有度量
d 的度量空間
X,
x 是
S 的內點,若對任意
r > 0,存在
y 屬於
S,且
d(
x,
y) <
r。
這個定義也可以推廣到
拓撲空間,只需要用
鄰域替代“開球”。 設
S 是拓撲空間
X 的
子集,則
x 是
S 的內點,若存在
x 鄰域被包含於
S。注意,這個定義並不要求鄰域是開的。
等價地,
S的內部是
S補集的
閉包的補集。內部的概念在很多情況下和閉包的概念對偶。
一個集合的
外部是它補集的內部,等同於它閉包的補集;它包含既不在集合內,也不在邊界上的點。一個子集的內部、邊界和外部一同將整個空間分為三塊(或者更少,因為這三者有可能是空集)。內部和外部總是
開的,而邊界總是
閉的。沒有內部的集合叫做
邊緣集。
拓撲學
設集合X及其冪集P(X),映射i: P(X)→P(X)稱為內部運算元,若且唯若其滿足以下內部公理:
其中對於X的子集A,i(A)稱為A的內部,i(A)中的點稱為A的內點。
從內部運算元出發可以定義拓撲,這和從開集,閉集,閉包,鄰域,導集,基等概念出發定義拓撲的方式是等價的。
開集
X的子集A稱為開集,若且唯若i(A)=A;
閉集
X的子集A稱為閉集,若且唯若i(X-A)=X-A;
閉包運算元,閉包,觸點
閉包運算元c:P(X)→P(X)定義為∀A⊆X,c(A)=X-i(X-A)。其中c(A)稱為A的閉包,c(A)中的點稱為A的觸點。閉包運算元是內部運算元的對偶概念,閉包是內部的對偶概念,觸點是內點的對偶概念。
鄰域
X的子集A,B,稱A是B的鄰域,若且唯若B⊆i(A)。
邊界,邊界點
邊界運算元∂
P(X)→P(X)定義為∀A⊆X,∂A=A-i(A)。其中∂A稱為A的邊界,∂A中的點稱為A的邊界點。
內點
這個定義可以推廣到
度量空間X的任意子集
S。具體地說,對具有度量
d的度量空間
X,
x是
S的內點,若對任意不屬於
S或在
S邊界上的
y,都有
d(
x,
y) >0。
這個定義也可以推廣到
拓撲空間,只需要用
鄰域替代“開球”。 設
S是拓撲空間
X的子集,則
x是
S的內點,若存在
x鄰域被包含於
S。注意,這個定義並不要求鄰域是開的。
集合的內部
集合 S 的內部是 S 的所有內點組成的集合。S 的內部寫作 int(S)、Int(S) 或 S int(S) 是 S 的開子集。
int(S) 是包含於 S 的最大的開集。
int(int(
S)) = int(
S)。(
冪等)
若 S 為 T 的子集,則 int(S) 是 int(T) 的子集。
若 A 為開集,則 A 是 S 的子集,若且唯若 A 是 int(S) 的子集。
有時候,上述第二或第三條性質會被作為拓撲內部的定義。
結論和性質
舉例
在任意空間,空集的內部是空集。
對任意空間 X, int(X) = X.
若
X 為
實數的歐幾里德空間
R,則 int([0, 1]) = (0, 1)。
若
X 為實數的歐幾里德空間
R,則
有理數集合
Q 的內部是空集。
若
X 為
複平面C =
R 在任意歐幾里德空間,任意
有限集合的內部是空集。
在實數集上,除了標準拓撲,還可以使用其他的拓撲結構。
若 X = R,且 R 有下限拓撲,則 int([0, 1]) = [0, 1)。
若考慮 R 中所有集合都是開集的拓撲,則 int([0, 1]) = [0, 1]。
若考慮 R 中只有空集和 R 自身是開集的拓撲,則 int([0, 1]) 是空集。
上述示例中集合的內部取決於背景空間的拓撲。接下來給出的兩個示例比較特殊。
在任意
離散空間中,由於所有集合都是開集,所以所有集合都等於其內部。
在任意
不可分空間X 中,由於只有空集和
X 自身是開集,所以 int(
X) =
X 且對
X 的所有
真子集A,int(
A) 是空集。
內部運算元
還有
因此,通過把集合替代為它的補集,閉包運算元和庫拉托夫斯基閉包公理的抽象理論可以輕易的轉換到使用內部運算元的語言中。