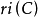基本介紹
- 中文名:相對內部
- 外文名:relative interior
- 所屬學科:數學
- 相關概念:凸集分離定理,仿射包等
定義,相關性質定理,
定義
有些凸集的內部是空的,然而把它作為其仿射包的子集考慮時,內部卻是不空的。例如,設 ,其中
,其中 ,在
,在 中,
中,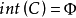 。然而在仿射包
。然而在仿射包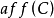 中考慮時,C的內部是不空的,因此引入凸集的相對內部的概念。
中考慮時,C的內部是不空的,因此引入凸集的相對內部的概念。



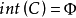
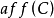
對於前面提到的凸集 ,它的相對內部與相對邊界分別是:
,它的相對內部與相對邊界分別是:

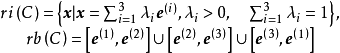
相關性質定理
關於凸集C的相對內部與相對邊界有以下性質。
性質1設 ,若C為凸集,而且
,若C為凸集,而且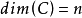 ,則
,則

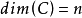
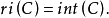

性質2設 ,若C為凸集,則
,若C為凸集,則

1.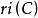 是凸集;
是凸集;
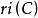
2.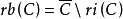 。
。
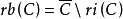
性質3設 ,若C為有界凸集,則
,若C為有界凸集,則


性質4設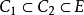 ,
,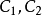 均為凸集,而且
均為凸集,而且 ,則
,則
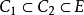
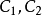


定理1 設 是凸集。
是凸集。

1. 若 ,則
,則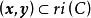 ;
;

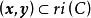
2.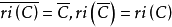 。
。
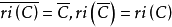
定理2 設 是凸集,
是凸集,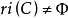 ,則,
,則,

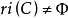
1. ;
;

2.  ;
;

3. ;
;

4.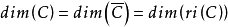 。
。
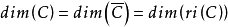
定理3 設 為非空凸集,
為非空凸集, ,則
,則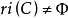 。
。


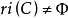
定理4 設 為非空凸集,則點
為非空凸集,則點 的充分必要條件是:
的充分必要條件是: 存在
存在 ,使
,使




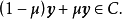
定理5 設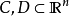 均為非空凸集,
均為非空凸集,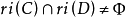 ,則
,則
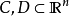
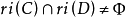
1.  ;
;

2.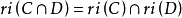 。
。
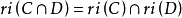
定理6 設 為非空凸集,
為非空凸集, 為由
為由 到
到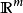 的線性映射,則
的線性映射,則



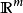
1. ;
;

2.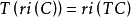 。
。
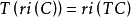
定理7 設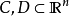 為凸集,且
為凸集,且 ,則,
,則,
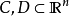

1. ;
;

2.  。
。