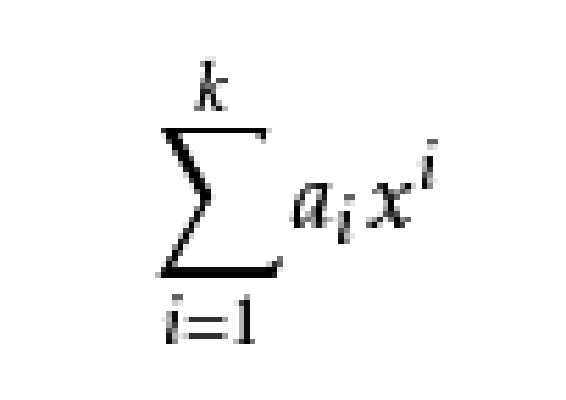仿射包

仿射包(affine hull)是由實線性空間中的集合所生成的仿射集，設A為實線性空間X中的集合，那么包含A的最小仿射集稱為A的仿射包。它是所有包含A的仿射集的全體的交集，也是A中的元素的不斷用直線連結後的元素全體，A的仿射包通常記為aff A。

基本介紹

• 中文名：仿射包
• 外文名：affine hull
• 所屬領域：凸分析、組合學
• 記法：A的仿射包通常記為aff A
• 相關概念：仿射集、凸包。仿射組合等

基本介紹

仿射包(affine hull)是由實線性空間中的集合所生成的仿射集，設A為實線性空間X中的集合，那么包含A的最小仿射集稱為A的仿射包。它是所有包含A的仿射集的全體的交集，也是A中的元素的不斷用直線連結後的元素全體，A的仿射包通常記為aff A。

仿射包(affine hull )是指由一個點集導出的一類點集。對於Eⁿ中的子集A，A的仿射包，記為Aff A，為A的任意有限多個元素x¹，x²，…，x^k的仿射組合

構成的集合。一個線性組合

稱為仿射組合，若係數αi (i=1，2，…，k)滿足

當A={x¹，x²}時，Aff A為通過x¹，x²的直線；當A={x¹，x²，x³}時，Aff A為通過x¹，x²，x³的平面。

n 維歐氏空間Rⁿ中的仿射集M 指的是具有x+S 形式的集合，其中x 是某個向量，而S 是由M 唯一確定的一個子空間，並稱為平行於M的子空間。換言之，一個集合M 稱為是仿射的，如果它包含所有穿過滿足x，y∈M 且x≠y 條件的點對x，y 的直線。如果X 是Rⁿ的子集，X 的仿射包(affine hull)，記作aff(X)，是指包含X 的所有仿射集的交集。注意aff(X) 本身是仿射集並且它包含conv(X)，aff(X) 的維數定義為平行於aff(X) 的子空間的維數。可以證明：aff(X)=aff(conv(X))=aff(cl(X))，進而凸集C 的維數定義為它的仿射包aff(C) 的維數。

相關概念

凸包

令X 為n 維歐氏空間Rⁿ的非空子集，集合X 的凸包(convex hull)，記作conv(X)，是指包含X的所有凸集合的交集，並且該集合是凸集X 的元的凸組合(convex combination) 是具有 形式的向量，其中m 為正整數， 屬於X,而 是標量，並滿足

條件。注意凸組合屬於conv(X) 。對於任意的凸組合以及在conv(X)上為凸的函式 我們有

這個關係是有名的Jensen 不等式的特例，Jensen 不等式在套用數學和機率論中有著廣泛的套用。

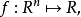
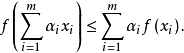
仿射集

設L是V的一個線性子空間， ,則L沿 的平移 稱為V的一個仿射集(affine set)。

仿射集 的維數等於線性子空間L的維數，即dim( 。

設中所有包含A的仿射集之交稱為A的仿射包(affine hull )，記為aff(A).A的維數定義為aff(A)的維數，即dim(A)=dim(aff( A))。

仿射組合

設稱為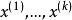的仿射組合。

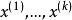
相關性質定理

定理1

設 則M是仿射集等價於M包含通過任意兩點 的直線，即

推論1

均為仿射集，則交集是仿射集。

推論2

若M是仿射集，則M必為凸集。

定理2

設則A的仿射包aff(A)等於A 中元素的有限仿射組合的全體。