凸組合是一類特殊的線性組合,是若干個點的某種特定意義下的非負線性組合。
基本介紹
- 中文名:凸組合
- 外文名:convex combination
- 別稱:凸線性組合
- 所屬學科:數學
- 性質:線性組合
定義
凸集與凸組合

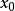
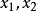
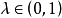
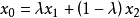
凸組合的幾何意義
直線上的情況


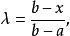
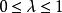




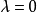
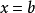

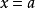
 圖1
圖1兩個向量的凸組合
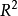

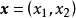
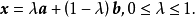
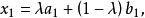
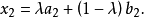

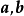
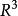
三個向量的凸組合

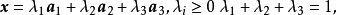


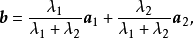
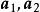
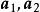
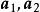

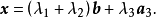

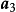
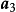






 圖2
圖2 圖3
圖3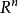
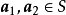
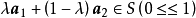

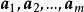
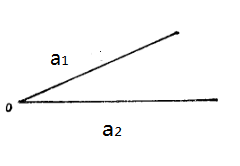 圖4
圖4相關性質定理
定理1
定理2
定理3
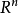

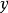


凸組合是一類特殊的線性組合,是若干個點的某種特定意義下的非負線性組合。

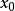
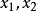
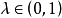
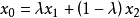
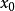


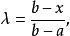
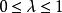




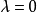
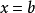

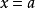
 圖1
圖1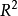

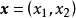
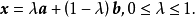
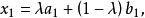
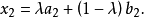

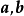
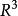

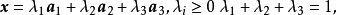


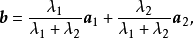
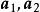
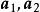
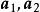

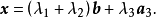

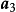
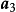






 圖2
圖2 圖3
圖3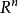
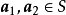
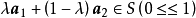

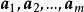
 圖4
圖4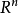

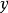

凸組合是一類特殊的線性組合,是若干個點的某種特定意義下的非負線性組合。...... 凸組合是一類特殊的線性組合,是若干個點的某種特定意義下的非負線性組合。[1] ...
在凸幾何中,凸集(convex set)是在凸組合下閉合的仿射空間的子集。更具體地說,在歐氏空間中,凸集是對於集合內的每一對點,連線該對點的直線段上的每個點也在該...
⒈對於一個集合D,D中任意有限個點的凸組合的全體稱為D的凸包。⒉對於一個集合D,所有包含D的凸集之交稱為D的凸包。可以證明,上述兩種定義是等價的概念...
令X 為n 維歐氏空間Rn的非空子集,集合X的凸包(convex hull),記作conv(X),是指包含X的所有凸集合的交集,並且該集合是凸集X 的元的凸組合(convex combination...
X稱為X1,X2,···,Xk的凸組合。這定理說明若問題有兩個或多於兩個的最優解,則它就有無窮多個最優解。另外,若問題的可行域無界,則可能無有限解,也可能有...
該劇講述的是官司勝訴率高達100%卻性格偏執的律師古美門研介,和坦率得有些魯莽的後輩黛真知子這對“凹凸組合”一起解決疑難案件的故事。[1] 續集《LEGAL HIGH ...
卡拉西奧多里定理(Caratheodory theorem )有限維凸集的表示定理.該定理斷言,n維空間中的凸集中的每一點都可用該集合的不超過n+l個點的凸組合來表示。...
定位柱是用於塑膠模具中精準鎖定模組與模板之間的位置以使模具順利工作的一種模具配件。定位柱為上定位塊與下定位塊凹凸組合配置,按照凸定位柱不同分為斜定位柱與...
此展品為紅山文化時期文物。玉呈青黃色,帶黃褐色沁。該器突破了一般勾雲形玉器長方形或抹角方形,當中鏤空作勾雲形卷角,四隅分布勾角,周邊伸出數量不等的小凸的...
