一類特殊的凸集被稱之為凸錐,它有極其重要的性質和套用。既是錐又是凸集的點集稱之為凸錐。常見的凸錐包括:二維平面中的半射線、整個n維歐式空間等。凸錐中有一個重要的定理,凸錐分離定理。
基本介紹
- 中文名:凸錐
- 外文名:Convex cone
- 基礎知識:凸集、錐
- 常見凸錐:二維平面中半射線、n維歐式空間
- 重要定理:凸錐分離定理
- 套用學科:凸理論基礎
基礎知識
凸集
錐




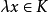


定義




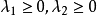


性質
簡單性質

凸集分離定理

典例
例1

例2


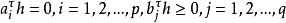







一類特殊的凸集被稱之為凸錐,它有極其重要的性質和套用。既是錐又是凸集的點集稱之為凸錐。常見的凸錐包括:二維平面中的半射線、整個n維歐式空間等。凸錐中有一個重要的定理,凸錐分離定理。




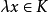






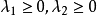







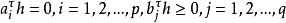






一類特殊的凸集被稱之為凸錐,它有極其重要的性質和套用。既是錐又是凸集的點集稱之為凸錐。常見的凸錐包括:二維平面中的半射線、整個n維歐式空間等。凸錐中有...
正錐是偏序群的正元素集,若G是偏序群,則G的正元素集G+={g∈G|g>0}及G的負元素集G-={g∈G|g<0}分別稱為G的正錐及負錐。G+滿足三個條件: 1.G++...
閉凸錐包(closed convex cones hull)一種凸錐.設S是線性空間中的集合,則稱包含S的最小的閉凸錐為S的閉凸錐包,或稱由S生成的閉凸錐,記為C(S>. ...
對偶錐((dual cone)亦稱極錐,錐的極集。有時對偶錐也稱為負極錐,相應地也可定義正極錐。實線性空間的理論常可推廣到凸錐的情形,即通常的向量的線性組合概念可...
閘錐就是 A 的支撐函式的有效域。當集合是包含原點的閉凸集時,閘錐就是回收錐的對偶錐。反之,如果回收錐的內部非空,那么它也是閘錐的對偶錐。...
凸組合是一類特殊的線性組合,是若干個點的某種特定意義下的非負線性組合。...... 中的凸錐如圖4所示。[3] 圖4 凸組合相關性質定理 編輯 凸組合定理1 集合X是...
凸錐頭蟲是一種昆蟲,屬於春蟲科...... 凸錐頭蟲是一種昆蟲,屬於春蟲科 中文學名 凸錐頭蟲 界 動物界 目 編織蟲目 科 春蟲科 亞科 春蟲亞科 屬...
若錐中的任一元素都可以表示成固定有限個元素的非負組合,則稱該錐為有限生成錐。...... 若錐K為凸集,則稱K為凸錐。若錐K中的任一元素都可以表示成固定有限...
凸對策(convex game)是一類有特殊贏得函式的對策,如果對於局中人Ⅰ的任意純策略x∈X,贏得函式A(x,y)是y的一個凸函式,稱此對策G為凸對策。...
回收錐(recession cone)是一種有關實線性空間中集合的特殊的錐。設A是實線性空間X中的集合,A的所有回收方向組成的集合稱為A的回收錐,閉集的回收錐有時稱為...
《現代經濟理論中的凸分析》是2005年7月由齊玲編輯出版的圖書。...... 本書作為一部數理經濟學專著,緊密貫穿最最佳化主題,從基礎的凸集、凸錐到凹函式與擬凹函式,...
在凸幾何中,凸集(convex set)是在凸組合下閉合的仿射空間的子集。更具體地說,在歐氏空間中,凸集是對於集合內的每一對點,連線該對點的直線段上的每個點也在該...
給定正整數n和非負整數m,記V為n維實歐氏空間Rn中以原點為頂點的開凸錐,又設V不包含整條直線,則Cn中的域D(V)={z∈Cn|Imz∈V}稱為錐V上第一類西格爾域...
1 簡介 2 泛函分析 3 凸錐 紹凱表現定理簡介 編輯 紹凱表現定理是對應於馬丁積分表現的一個著名的泛函分析定理。紹凱表現定理的要點是:在一個局部凸的豪斯多夫...
紹凱積分表示理論(Choquet theory of integralrepresentation)是基於凸集和凸錐理論的積分表示理論。在緊凸集情形,紹凱積分表示定理是克列因-米爾曼定理的推廣。...
1 簡介 2 掃除空間 3 凸錐 自然分解公理簡介 編輯 自然分解公理是判定掃除空間的四條公理之一。若u,f,g∈𝓦使得u≤f+g,則存在v,w∈𝓦使得u=v+w...
