回收錐

回收錐(recession cone)是一種有關實線性空間中集合的特殊的錐。設A是實線性空間X中的集合，A的所有回收方向組成的集合稱為A的回收錐，閉集的回收錐有時稱為漸近錐。當集合為凸集時，其回收錐為凸錐；當集合為包含原點的閉凸集A時，其回收錐即∩_λ≥0λA，有時也對任意集合A，稱如上定義的集合為其回收錐。

巴拿赫空間的非空閉凸集有界的充分必要條件為其回收錐只包含原點。因此，經常利用回收錐來證明一個閉凸集的有界性。

基本介紹

• 中文名：回收錐
• 外文名：recession cone
• 所屬學科：數學
• 所屬領域：凸分析
• 相關概念：回收空間、巴拿赫空間、閉凸集等

基本介紹

給定非空凸集C，我們說向量d是C的一個回收方向(direction ofrecession)，如果對所有的和都成立。因此，d是C的一個回收方向，如果我們從C中任意的x點出發，沿著d的方向走到無窮，而永遠都不穿過C的相對邊界跑到C之外的點上去。

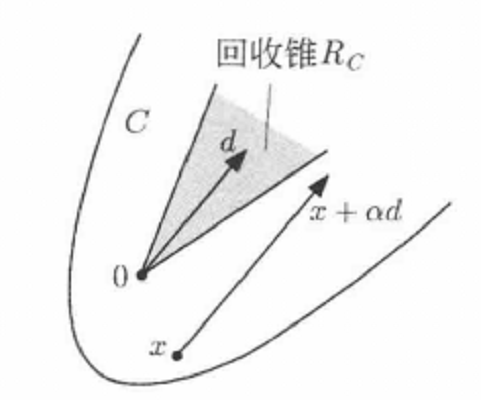
所有回收方向的集合是一個包含原點的錐體(core)，我們稱它為C的回收錐(recession cone)，並記作(參見圖1)。於是，如果對所有的和成立。閉凸集的一條重要性質就是為檢驗是否成立，只需要驗證對單一的成立就可以了。這就是下述命題的(b)部分。

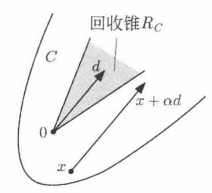圖1

圖1 凸集C的回收錐的圖示。回收方向d滿足對所有和成立。

回收錐定理

命題1(回收錐定理(Recession Cone Theorem))令C為非空閉凸集。

(a) 回收錐是閉的和凸的。

(b) 向量d屬於若且唯若存在向量使得對所有成立。

證明：(a) 如果屬於而是正的標量使成立，我們有對任意的和

其中最後的包含關係成立是因為C是凸的，而根據的定義和屬於C。於是這表明是凸的。

令d屬於的閉包，並令為收斂到d的點列。對於任意的和，我們有對所有k成立，並且因為C是閉的，。於是，從而是閉的。

(b) 如果，根據的定義，每個向量都具有所要求的性質。反之，令d使得存在向量滿足對所有成立。不失一般性，假定d≠0。任取和，我們要證明。事實上，只要證明，即假定，因為通過用代替d可以把的一般情形可以歸結為的情況。

根據我們對x和d的選取，令

可知對所有k成立，如果對某個k成立，那么就屬於C，而我們的證明完成。因此假設對所有k成立，並且定義

使得是以為球心以為半徑的球面與從出發通過的射線的交點(參見圖2中的構造方法)，現在我們來論證,，並且對於充分大的k，，於是利用C的閉性，可導出。

的確，據的定義，我們有

因為是無界點列，

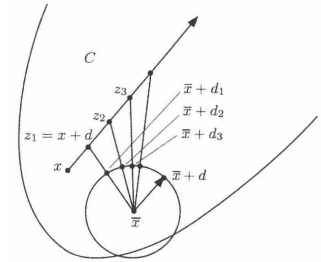圖2

圖2 命題1(b)的證明中用到的構造。

於是結合前面的關係，我們有對所有滿足的k，在連線的線段上，向量處在和之間，因此由C的凸性，我們有對所有充分大的k成立。因為和C是閉的，可知。

上述命題中集合C為閉的假設是實質性的。如果沒有這個假設，(a)部分不成立的一個例子是，考慮集合

它的回收錐等於C，而它是非閉的。該例子中(b)部分也不成立，因為對於方向d=(1，0)，我們有對所有和除之外的所有成立。

回收錐其他性質

下述命題給出回收錐的一些其他性質。

(回收錐的性質)令C為非空閉凸集。

(a) 包含一個非零的方向若且唯若C是無界的。

(b)。

(c) 對任意一組閉凸集，其中為任意指標集，並且我們有

(d) 令W為m維歐氏空間的一個緊的凸子集，並令A為m×n維矩陣，集合

(假設該集合為非空) 的回收錐是其中是A的化零空間(nullspace)。