回收方向(direction of recession)是指實線性空間的集合中的射線所定義的方向。設A為實線性空間X的集合,若h∈X且存在x∈A,使得對於任何λ≥0,有x+λh∈A,那么h稱為A的回收方向。
基本介紹
- 中文名:回收方向
- 外文名:direction of recession
- 所屬學科:數學
- 所屬問題:凸分析(凸集)
- 相關概念:回收錐、凸集等
定義
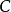
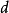
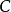

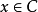
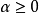
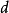
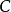
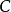

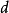
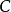
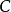
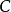
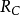


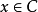
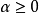


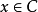
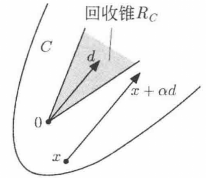 圖1
圖1分析理解

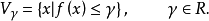
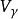

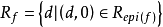
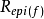
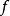
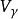

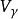

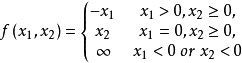
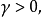
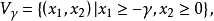

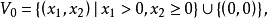
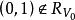




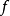
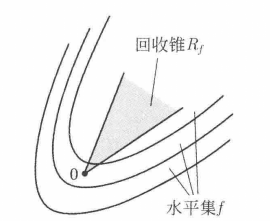 圖2
圖2
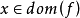


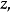


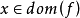




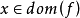


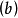
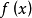



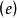
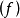
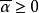

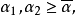
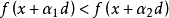

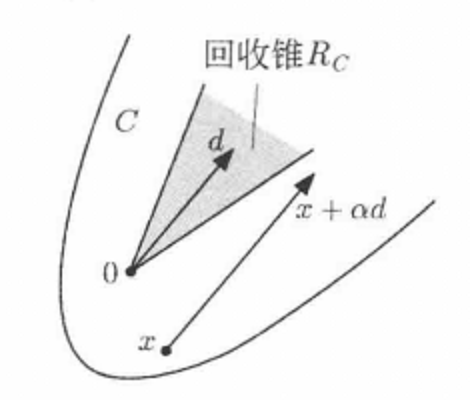
回收方向(direction of recession)是指實線性空間的集合中的射線所定義的方向。設A為實線性空間X的集合,若h∈X且存在x∈A,使得對於任何λ≥0,有x+λh∈A,那么h稱為A的回收方向。
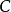
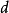
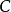

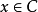
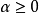
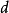
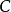
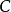

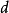
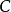
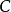
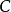
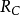


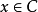
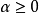


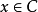
 圖1
圖1
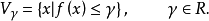
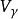

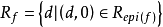
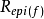
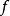
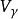

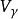

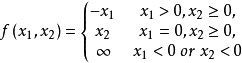
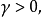
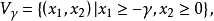

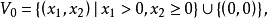
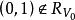




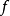
 圖2
圖2
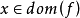


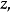


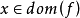




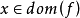


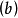
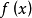



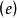
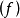
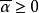

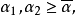
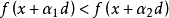

回收方向(direction of recession)是指實線性空間的集合中的射線所定義的方向。設A為實線性空間X的集合,若h∈X且存在x∈A,使得對於任何λ≥0,有x+λh∈A,...
回收錐(recession cone)是一種有關實線性空間中集合的特殊的錐。設A是實線性空間X中的集合,A的所有回收方向組成的集合稱為A的回收錐,閉集的回收錐有時稱為...
HC-130H增大航程的空中搜尋救援回收型,從 C-130H 改進而來。正常載油量同 C-130E,這種特種型號飛機的特點是裝有大功率的 3,661 當量千瓦艾利遜 T56-A-15 ...
核能發電是核能運用的重要方向之一。然而核能發電會產生大量的氣體、液體、固體的...建設現代文明城市,人民不可不重視廢物的處理,最有效的就是廢物回收和再利用,...
動能回收系統是FIA在F1賽車上使用的一項新技術,英文縮寫KERS.原理是:通過技術手段將車身制動能量存儲起來,並在賽車加速過程中將其作為輔助動力釋放利用。...
回收物流(returned logistics)指不合格物品的返修、退貨以及周轉使用的包裝容器從需方返回到供方所形成的物品實體流動。即企業在生產、供應、銷售的活動中總會產生各種...
塑膠製品回收標識,由美國塑膠行業相關機構制定。這套標識將塑膠材質辨識碼打在容器或包裝上,從1號到7號,讓民眾無需費心去學習各類塑膠材質的異同,就可以簡單地...
中國回收交易網是一個再生資源回收行業電子商務入口網站,是以網路信息服務為主,致力於推進廢舊物資回收、再生資源利用的企業和個人利用網上綜合平台進行商務交流、產品...
細沙回收系統的主要作用是對砂石清洗、脫水、分級,能夠很好的回收傳統制砂行業中洗砂機流失的大量細砂,提升經濟效益的同時,降低了尾料的處理費用及流失細砂會環境...
資金回收是指企業取得經營收入,收回墊支資金。在正常情況下,資金回收額要大於資金耗費額,這個差額就是企業實現的生產經營成果。資金的順利回收,既是補償資金耗費的...
廢錫又稱為再生錫。廢錫回收是指生活中的錫廢棄物或工業生產過程中的錫金屬廢料等。再生錫是從回收錫廢雜物料冶金過程後得出的技術,煉化再生錫的廢雜物料包括鐵...
富爾頓地對空回收系統(英文:Fulton surface-to-air recovery system,縮寫:STARS)是由美國中央情報局、美國空軍和美國海軍所採用的一套利用單架MC-130E Combat ...
太空飛行器回收系統,是太空飛行器上為回收而設定的各種裝置的組合。回收屬太空飛行器返回過程的最後階段──著陸階段。種類太空飛行器經專門減速裝置減速後,以一定速度安全著陸稱為軟...
香港回收門事件啟示 編輯 香港捐款的“較真”行為給我們一個深刻的啟示:支撐現代...慈善捐贈的發展,制度化的發展方向才是保障。首先,慈善立法是我們應當倍加重視的...
2016年5月5日,商務部、國家發展改革委、工業和信息化部、環境保護部、住房城鄉建設部、供銷合作總社印發《關於推進再生資源回收行業轉型升級的意見》。該《意見》分...
制動能量回收系統(Braking Energy Recovery System)是指一種套用於汽車或者軌道交通上的,能夠將制動時產生的熱能轉換成機械能,並將其存儲在電容器內,在使用時可迅速...
尤其是固定資產的可折舊度、無形資產的攤銷額以及將要報廢和不可回收的資產等...現象,相信巨大成功是偶爾現象時,機率和預期值方程才開始向著對自己有利的方向...
的等級系統,向人盡其才、人盡其用、按勞取酬、按能取酬、按智取酬的方向努力...二氧化碳回收和固廢綜合利用等多項環保工程改造;生產過程產生的污水全部達標排放,...
