閘錐

閘錐就是 A 的支撐函式的有效域。當集合是包含原點的閉凸集時，閘錐就是回收錐的對偶錐。反之，如果回收錐的內部非空，那么它也是閘錐的對偶錐。

基本介紹

• 中文名：閘錐
• 外文名：barrier cone
• 適用範圍：數理科學

定義

設 C 為 中的凸集。C 的閘錐指所有滿足如下條件 的全體：存在 ，對所有 ，均有 。

性質

閘錐是實線性空間的集合的極集所生成的錐。設 A 為巴拿赫空間 X 的集合，X^*為 X 的對偶，那么 A 的閘錐可表示為。

因此，閘錐就是 A 的支撐函式的有效域。當集合是包含原點的閉凸集時，閘錐就是回收錐的對偶錐。反之，如果回收錐的內部非空，那么它也是閘錐的對偶錐。

凸集

簡介

在凸幾何中，凸集(convex set)是在凸組合下閉合的仿射空間的子集。更具體地說，在歐氏空間中，凸集是對於集合內的每一對點，連線該對點的直線段上的每個點也在該集合內。例如，立方體是凸集，但是任何中空的或具有凹痕的例如月牙形都不是凸集。

特別的，凸集，實數R上（或複數C上）的向量空間中，如果集合S中任兩點的連線上的點都在S內，則稱集合S為凸集。

凸錐

一類特殊的凸集被稱之為凸錐，它有極其重要的性質和套用。既是錐又是凸集的點集稱之為凸錐。常見的凸錐包括：二維平面中的半射線、整個n維歐式空間等。凸錐中有一個重要的定理，凸錐分離定理。

設是中的點集，若點集既是錐又是凸集時，即當時，對任意不同時為零的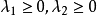，點，則稱為凸錐。